Correctly count all unique near-coincident hexagonal lattice pairs?

Question

My earlier question How should I restrict the points considered in each hexagonal lattice to correctly count all unique near-coincident lattices? turns out to have an excellent and instructive answer, primarily because I'd left out part of the question I'd planned on posting.

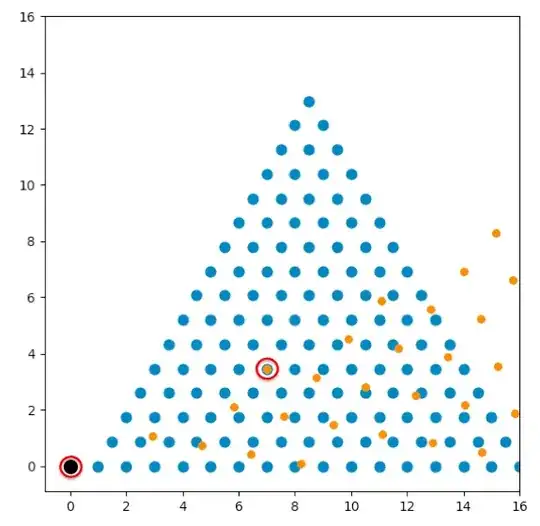
Please see How should I restrict the points considered in each hexagonal lattice to correctly count all unique near-coincident lattices? for the setup to this question, but now with the added constraint that the absolute values of the indices $(i, j), (k, l)$ will be limited to some finite size with a parameter $n_{max}$ such that $|i| \le n_{max}$, $|j| \le n_{max}$ and $|i+j| \le n_{max}$ which forms a hexagonally bound array of points when $x = a \left(i + \frac{1}{2} j\right)$ and $y = a \frac{\sqrt{3}}{2} j$.

A further constraint for my problem is that $a_2/a_1$ is irrational and fixed. This is the reason for the finite $\delta$. For a small $n_{max}$ there are usually no solutions, but opening up $\delta$ to say 0.01 allows for some near-coincident lattice matchings; we're essentially stretching or compressing the 2nd lattice to "make it coincident" with the first.

---

Question: How should I restrict the points considered in each hexagonal lattice to correctly count all unique near-coincident lattices when $(i, j)$ are limited by $n_{max}$ as described above?

I know I should restrict my search to a pie-shaped segment of all points in each of the two lattices, perhaps a 30° slice of one against a 60° slice of the other, but I haven't been able to convince myself that this guess is mathematically sound.

---

Example of a proper coincident lattice: $(i, j), (k, l) = (5, 4), (2, 3)$ with $\frac{a_2}{a_1} = \sqrt{\frac{61}{19}}$ and $n_{max} = 16$ with cuts at $0 \le \theta_{ij} < 60°$ and $0 \le \theta_{kl} < 30°$. This finds exactly one coincidence point. Are these angle restrictions correct to find all near-coincident solutions? Ignoring solutions with lowest common denominators $LCD(i, j, k, l) > 1$ will help avoid some redundancies.

Answer 1

If you're trying to pick points geometrically you are working too hard.

here's how it's really done, with the example of finding a decent match for a size ratio of $x = \pi$.

In this we will be iterating over the Loeschain numbers, which is equivalent to considering points in order of euclidean distance from the origin.

We'll start with $a_2=1$, using $k=1$ and $\ell=0$. We now find lower and upper $a_{1-}$, $a_{1+}$ and corresponding $i_-,j_-, i_+, j_+$ by starting at $\lfloor x^2 \rfloor$ and $\lceil x^2 \rceil$ and going down and up respectively until we land on Loeschian numbers. Then $p = a_{1-}/a_2$ and $q = a_{1+}/a_2$ are our current best approximations -- well, the squares of the best approximations; working with integers is less of a pain in general.

Repeatedly: increment $a_2$ to the next Loeschian number. Calculate $a_2x^2$ again, and also $a_2p$ and $a_2q$. Starting at $\lfloor a_2x^2 \rfloor$ and $\lceil a_2x^2 \rceil$, again go down and up respectively to find Loeschian numbers... but if you reach $a_2p$ or $a_2q$ before that happens, give up: something earlier worked better. On the other hand, if you do find one, then you can update $p$ or $q$ as appropriate.

This can go on forever, so long as it's never true that $a_2x^2$ is itself a Loeschian number; in that case you've found an exact match.

---

So, for $\pi$:

• $\pi^2 \approx 9.9$, so our starting point is $p=9$, $q=12$
• $3\pi^2 \approx 29.6$, and we find $3\cdot9 < 28 < 3\pi^2 < 31 < 3\cdot12$, so now $p=28/3$, $q=31/3$
• $4\pi^2 \approx 39.5$, $4\frac{28}{3} < 39 < 4\pi^2 < 4\frac{31}{3}$ -- this time, we don't find a better upper bound, so only $p$ changes, to $\frac{39}{4}$.
• $7\pi^2 \approx 69.1$, and in this case we don't find any thing that improves the situation.
• Proceeding in this fashion we get $q = \frac{91}{9}$, $q = \frac{121}{12}$, $p = \frac{127}{13}$, $q=\frac{129}{13}$, $p = \frac{157}{16}$, $q=\frac{208}{21}$, and $q=\frac{247}{25}$, and so on.

Not all the numbers we get are optimal: $\frac{157}{16}$ isn't as good as $\frac{129}{13}$, but it is on the low side instead of the high side so we get to keep it for now to keep us on track.

Answer 2

I believe I've solved my problem but I don't know how to offer a formal proof for this.

It's clear that it is sufficient to include only the points in $0 \le \theta \le 30°$ from each lattice in order to find all possible lengths in each.

Each lattice is 6-fold symmetric so rotations from one lattice to the other are only unique within for example $-30° \le R \le 30°$ range, and every rotation at $+R$ will have a mirror point at $-R$

So use points in each lattice within $0 \le \theta \le 30°$ and for every rotation $\mod(R, 30°) \ne 0$ include a second rotation at $-R$.

plot: https://pastebin.com/fnxGV3Yc