I am trying to come up with a general algorithm to determine if two lattices are related to each other by a simple rotation operation.
The way I think about a lattice is as an array of points. The lattice is specified by a set of basis vectors. For example a 2D lattice can be defined by the following basis:
$$\mathcal{B} = \begin{bmatrix} \hat{e}_x & \hat{e}_y \end{bmatrix} \Lambda = \begin{bmatrix} \hat{e}_x & \hat{e}_y \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 2 & 5 \end{bmatrix} = \begin{bmatrix} \vec{b}_x & \vec{b}_y \end{bmatrix} $$
The lattice consists of all the points that can be expressed as integer linear combinations of the basis vectors: $l\vec{b}_x + m \vec{b}_y$, where $l,m \in \mathbb{Z}$. The lattice generated by the basis vectors $\vec{b}_x = \hat{e}_x + 2 \hat{e}_y$ and $\vec{b}_y = 5 \hat{e}_y$ is shown below.
Now suppose I am given two lattices with basis vectors as follows:
$\mathcal{B}_1 = \begin{bmatrix} \hat{e}_x & \hat{e}_y \end{bmatrix} \Lambda_1 = \begin{bmatrix} \hat{e}_x & \hat{e}_y \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 2 & 5 \end{bmatrix}$ and
$\mathcal{B}_2 = \begin{bmatrix} \hat{e}_x & \hat{e}_y \end{bmatrix} \Lambda_2 = \begin{bmatrix} \hat{e}_x & \hat{e}_y \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 3 & 5 \end{bmatrix}$.
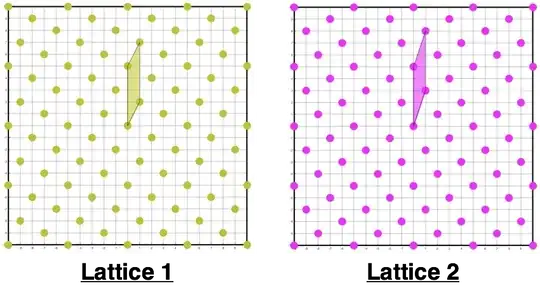
The two lattices are shown next to each other.
I want to determine if Lattice 2 is related to Lattice 1 by a simple rotation other than the identity operation. I perform a few checks first:
I check that their volumes (determinants) are the same. Otherwise, they define two distinct lattices and so one lattice cannot be obtained by a simple rotation of the other.
I also check that $\Lambda_1^{-1} \cdot \Lambda_2$ is not a UNIMODULAR MATRIX (a matrix of integers with determinant $\pm$1). If it is then the two bases define the same lattice.
If they are related by a simple rotation, there exists a rotation matrix $\mathbb{R} \in O(3)$ such that $\Lambda_2 = \mathbb{R} \Lambda_1 U$, where $U$ is a unimodular matrix (i.e. a matrix of integers with $\det(U)=\pm 1$).
In the above example, I know visually that the two lattices are related to each other by a rotation operation. However, I am not sure how to solve it using a code of some sort. The complication I think comes from the fact that any lattice has infinitely-many bases.
My solution: I assume a unimodular matrix with unknown integer entries $a,b,c,d$. I can use the properties of the rotation matrix (i.e. $\mathbb{R} \cdot \mathbb{R}' = I$, where $\mathbb{R}'$ is the transpose of the rotation matrix and $I$ is an identity matrix) and the unimodular matrix ($\det(U) = \pm 1$) and solve for $a,b,c,d$. If there exists a solution where all the entries are integers then the two lattices are related by a rotation operation.
EDIT: To make it clear, here is an example of two lattices that are not simple rotations of each other but the checks pass:
$\mathcal{B}_1 = \begin{bmatrix} \hat{e}_x & \hat{e}_y \end{bmatrix} \Lambda_1 = \begin{bmatrix} \hat{e}_x & \hat{e}_y \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 2 & 5 \end{bmatrix}$ and
$\mathcal{B}_2 = \begin{bmatrix} \hat{e}_x & \hat{e}_y \end{bmatrix} \Lambda_2 = \begin{bmatrix} \hat{e}_x & \hat{e}_y \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 5 \end{bmatrix}$.
I think this should work but it is very inefficient. I think there should be an efficient solution for this. Any suggestions are appreciated!