A parabola touches the bisectors of the angles formed by lines $x+2y+3=0$ and $2x+y+3=0$ at $(1,1)$ and $(0,-2)$. Find its focus and directrix.

Question

A parabola touches the bisectors of the angles obtained by the lines $x+2y+3=0$ and $2x+y+3=0$ at the points $(1,1)$ and $(0,-2)$. Then find its focus and the equation of the directrix.

My approach is as follows:

The equation of bisector is $$\frac{x+2y+3}{\sqrt{5}}= \pm \frac{2x+y+3}{\sqrt{5}}$$

We get the required bisectors as $x-y=0$ and $3x+3y+6=0$, or $x+y+2=0$.

$x-y=0$ is tangent to the parabola at $(1,1)$, whereas $x+y+2=0$ is tangent to the parabola at $(0,-2)$.

From here, how do I proceed?

Answer 1

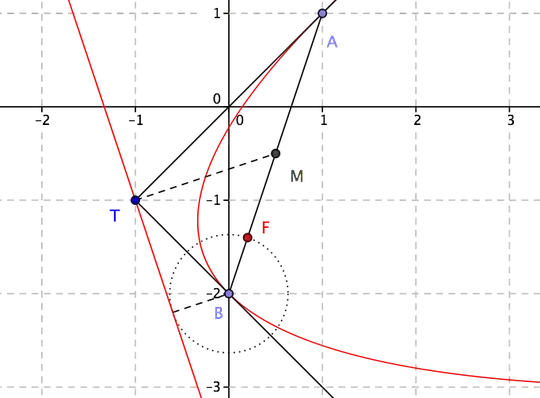
Given points $A=(1,1)$, $B=(0,-2)$, $T=(-1,-1)$ (which is the intersection point of the tangents), the parabola touching $AT$ at $A$ and $BT$ at $B$ can be constructed using this property of a parabola (see EDIT 2 at bottom for a proof):

The exterior angle between any two tangents is equal to the angle which either segment of tangent subtends at the focus.

Construct then the circle tangent to $AT$ at $T$ and passing through $B$, whose arc inside $\angle ATB$ is the locus of points at which $BT$ subtends an angle equal to the exterior angle. And similarly construct the circle tangent to $BT$ at $T$ and passing through $A$: the intersection of those circles, different from $T$, is the focus $F$ (see diagram below).

Finally, to construct the directrix, one can for example find the midpoint $M$ of $AB$ and subsequently the midpoint $P$ of $TM$, then $P$ is a point on the parabola and the directrix is the line perpendicular to $TM$ and intersecting $PT$ at a distance from $P$ equal to $PF$.

EDIT.

In this particular case things are even simpler, because tangents $AT$ and $BT$ are perpendicular: this implies that the directrix passes through $T$ and is perpendicular to line TM described above, while $AB$ is a focal chord (see here for a proof). Once the directrix is found, from points $A$ and $B$ it is easy to find focus $F$.

EDIT 2.

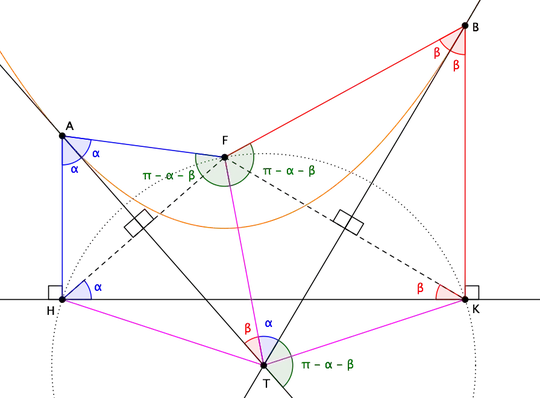
It may be useful to give a proof of the property mentioned at the beginning. Let then $F$ be the focus of the parabola, $A$, $B$ any two points on it, $H$, $K$ their projections on the directrix, $T$ the intersection point of the lines touching the parabola at $A$ and $B$ (see figure below).

As $AF=AH$ and $AT$ bisects $\angle FAH$, then $AT$ is the perpendicular bisector of $FH$ and $HT=FT$. Likewise, $FT=KT$ and $H$, $F$, $T$ belong to the same circle centred at $T$.

But $\alpha=\angle FAT=\angle HAT=\angle FHK$ (complementary of the same angle) and $\angle FHK=\angle FTB$ (inscribed angle and half of central angle subtending the same arc), hence $\angle FAT=\angle FTB=\alpha$. Similarly, $\angle FBT=\angle FTA=\beta$ and: $$ \angle AFT=\angle BFT=\pi-\alpha-\beta = \text{external angle formed by tangents $AT$ and $BT$.} $$

Answer 2

I have used the following properties derived from the basic equation of parabola.

(i)M is mid-point of AB. Line joining the point of intersection of tangents to the mid-point of the chord of contact is parallel to the axis of the parabola or perpendicular to the directrix.

(ii)Perpendicular tangents intersect on the directrix and the points of contact of tangents are the extremities of the focal chord.

(iii) The portion of tangent between the point of contact and the directrix always subtends a right angle at the focus.

Answer 3

Since angular bisectors are perpendicular to each other and are tangent to the parabola at $A(1,1)$ and $B(0,2)$, the point of intersection of the two given lines $(-1,-1)$ is a point on the directrix of the parabola.

The median through $P$ to the Archimedes triangle $PAB$ is known to be parallel to axis, which gives the slope of directrix as $-3$. So foot of perpendicular from $A$ on to directrix is $\left(-\dfrac{7}{5},\dfrac{1}{5}\right)$. This is also the image of the focus in the tangent $PA \equiv x-y=0$ which is easily found as $\boxed{\left(\dfrac{1}{5},-\dfrac{7}{5}\right)}$