0

Thanks for reading.

Every time I look for "intuitive" explanations of why trig derivatives and integrals are what they are, I always get graphics like the following:

enter image description here

However, Sines and Cosines show up in mathematical topics which aren't always geometric by nature...even if perhaps connections to triangles and circles can always be found.

Are there ways to explain, still intuitively (by intuitive I mean explanations that "click," I don't mean hand-wavy...I hope that makes sense), but non-geometrically, why the derivative of sine is cosine (and why the integral of cosine is sine, derivative of cosine is -sine, etc...)?

Thank you!

joshuaronis
  • 1,479
  • 10
  • 29
  • 2
    In order to answer this question, I would need to know how do you intuit sine and cosine themselves? One way of defining them is as solutions to the differential equation $f + f'' = 0$, in which case the derivatives are obvious. – Dark Malthorp Apr 28 '20 at 14:17
  • Did you mean something like $$\frac{\sin(x+h)-\sin(x)}h=\sin(x)\frac{\cos(h)-1}{h}+\cos(x)\frac{\sin(h)}{h}=-\sin(x)\frac{\sin^2(h)}{h(1+\cos(h))}+\cos(x)\frac{\sin(h)}{h}$$ which reduces everything to $\lim_{h\to0}\frac{\sin h}{h}=1$? – Lutz Lehmann Apr 28 '20 at 14:18
  • @DarkMalthorp but would you be able to see them as solutions to that differential equation BEFORE knowing their derivatives? If so, I'd love to see how they arise from that differential equation directly! That would definitely be in the right direction! – joshuaronis Apr 28 '20 at 14:19
  • @LutzLehmann maybe...but, I can't really follow... – joshuaronis Apr 28 '20 at 14:20
  • 1
    Your question, and your comment to @DarkMalthorp raises an issue: What definition of sine and cosine are you starting from? If you cannot accept an intuition based on an analytic definition, and you also cannot accept an intuition based on a geometric definition, then you are obliged to tell us: on the basis of what definition are we allowed to build our intuition for you? – Lee Mosher Apr 28 '20 at 14:26
  • What Lee Mosher said. Anyway, for a way forward you might explain if any of the derivations here would satisfy you? Which would and which would not? I think that any answer posted here should actually go there, so I vote to close as a duplicate. There may be scope for disagreement here. If so, please elaborate! Some answers there you probably have seen, some may be not? – Jyrki Lahtonen Apr 28 '20 at 14:30
  • See the question "Intuitive understanding of the derivatives of $\sin x$ and $\cos x$". This answer contains the geometric explanation you mention, but there are others. I'm personally fond of my answer, which is geometric in a different way. – Blue Apr 28 '20 at 14:59
  • 1
    Thank you @Blue !! Will defietely take a look at it – joshuaronis Apr 28 '20 at 15:03
  • @LeeMosher and that's my bad...I'm not very advanced...the only definition of sine and cosine I had was as the ratios in triangles....could you perhaps provide a link to a page with a bunch of definitions? Is there a question like that on Stack Exchange? I'd really appreciate it - that would be cool to look at! Thank you! – joshuaronis Apr 28 '20 at 15:04
  • @JyrkiLahtonen look at my comment above to LeeMosher^^^ Thank you!! – joshuaronis Apr 28 '20 at 15:05
  • @Blue You have the appropriate gold badge, and should be able to add the thread you linked to among the list of duplicate targets. If you don't mind, that would be a service to site hygiene. While we are at it, do you think that the thread I linked to should be closed as a duplicate of the older one? – Jyrki Lahtonen Apr 28 '20 at 16:37
  • @JyrkiLahtonen: Done! (I hadn't realized we could add links after a question had already been closed. This could be very useful! :) ... As for closing the not-quite-as-old question: It's asking for "different" ways of finding the derivatives, whereas the older (oldest?) one is asking for "intuitive" ways. That might be enough of a distinction to leave them both as-is, but my opinion isn't a strong one. I'll note that I already have a comment to the "different" question linking to the "intuitive" one. – Blue Apr 28 '20 at 16:56

2 Answers2

1

I always like to consider the graphical forms of the equations. For derivatives especially. For example, the derivative of $\cos{\theta}$ measures the slope of the function $\cos{\theta}$ itself. If you can imagine the graph of $\cos{\theta}$ you can immediately realise that it dips off at the start which implies a negative gradient. So, if the derivative describes a measure of the slope of a function, then if we were to graph the derivative of $\cos{\theta}$ against $\theta$, then the derivative function will have to start at negative values. As you may know, $\sin{\theta}$ and $\cos{\theta}$ are closely related in their derivatives. Normally, the equation of the form $\sin{\theta}$ starts with positive values, however, since the slope of the $\cos{\theta}$ graph is initially negative this means that the derivative of $\cos{\theta}$ must be $-\sin{\theta}$. Sorry that it's alot to take In, but this is what I do when investigating the derivatives of trigonometric functions. It might be worth while getting used to what each function looks like before using this thought process.

JayP
  • 1,096
1

It comes down to how you choose to define sine and cosine. There are multiple possible definitions, which are not obviously equivalent, but all give rise to the same functions and therefore can all be used to intuit $\frac{d}{dx} \sin(x) = \cos(x)$ and $\frac{d}{dx} \cos(x) = -\sin(x)$. I'll go through the three most common definitions:

Geometric definition:

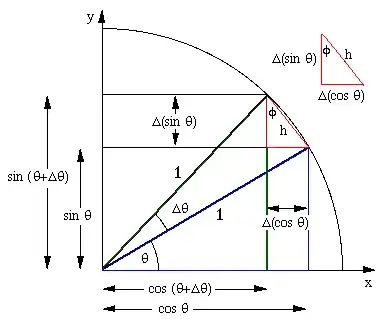
If you're working with the geometric definitions for sine and cosine, then the geometric proof for their derivatives is clearly the most intuitive. Whether or not it is intuitive to you is a function of your intuition for geometry and calculus, not the sine and cosine functions specifically.

Differential equations:

As I mentioned in the comments, you can define sine and cosine as solutions to the differential equation $$ f(x) + f''(x) = 0 $$ with the initial value conditions $\sin(0) = 0$, $\sin'(0) = 1$ and $\cos(0) = 1$, $\cos'(0) =0$. If you've got a good intuition for differential equations, it ought to click that this uniquely defines $\sin(x)$ and $\cos(x)$. It might not be clear it's equivalent to the geometric definition. But it's trivially in this case that $\sin'(x) = \cos(x)$ and $\cos'(x) = -\sin(x)$. We observe $\sin'(x)$ solves the same differential equation, because we can differentiate both sides of $\sin(x) + \sin''(x) = 0$ and see that $$ \sin'(x) + \sin'''(x) = 0 $$ and then we also observe that $\sin'(x)$ has the initial values $\sin'(0) = 1$ and $\sin''(0) = -\sin(0) = 0$, so $\sin'(x)$ satisfies the same initial value problem as $\cos(x)$ and hence they are equal. Similarly, you can convince yourself $\cos'(x) = -\sin(x)$.

Complex analysis:

I doubt there are many people for whom this is more intuitive than the other two definitions, but I'll include it for the sake of completeness. For real $x$, we can define sine and cosine to be the real-analytic functions such that Euler's identity $e^{i x} = \cos x + i\sin x$ is true, i.e.:$$ \sin(x) = \Im (e^{i x})\\ \cos(x) = \Re (e^{i x}) $$ Then \begin{eqnarray} \frac{d}{dx} e^{i x} &=& \frac{d}{dx}\left(\cos(x) + i\sin(x)\right)\\ i e^{i x} &=& \cos'(x) + i\sin'(x)\\ i(\cos(x) + i \sin(x)) &=& \cos'(x) + i\sin'(x)\\ -\sin(x) +i\cos(x) &=& \cos'(x) + i \sin'(x) \end{eqnarray} Equating real and imaginary parts yields the desired identity.

Dark Malthorp
  • 5,945