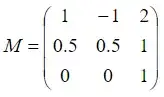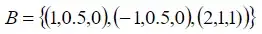0

We have a quadratic form in the reals.

$$ q(x,y,z) = 2zx + 4yz - 2xy $$

($q$ is in the standard form of $V = R^3$)

We need to find: $(1)$ A base for $V$ in which $q$ is diagonalized. $(2)$ Find a subspace $W$ of $V$ with maximal dimension such that $q(w) \geq 0, \forall w \in W$

I am stuck in undertanding $(2)$.

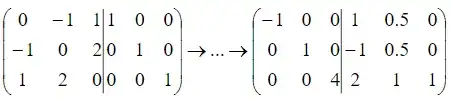
$(1)$ Using elemtaric congruence we get:

enter image description here

Therefore our change of base matrix is:

enter image description here

Now we can show the base in which $q$ is diagonalaized:

enter image description here

NOW THE PROBLEM STARTS

They choose the subspace: $$ W = Sp \{(-1,0.5,0),(2,1,1)\} $$

Now they say: $$ \forall w \in W: [w]_{B} = (0, \lambda_1, \lambda_2) $$

Therefore: $$ q(w) = -1 \cdot 0^2 + \lambda_1^2 + 4 \lambda_2^2 \geq 0 $$

I dont understand

  1. How did they know to take that subspace?

  2. How $[w]_B = (0, \lambda_1, \lambda_2)$

How did they know?

Thank you.

Alon
  • 1,647
  • Please use MathJax to format your mathematical expressions instead of pasting pictures of them. This question is almost incomprehensible without those images, which makes it inaccessible to people who depend on screen readers. Moreover, images are neither searchable nor show up in summaries. – amd Apr 26 '20 at 22:22

2 Answers2

1

Take a look at your diagonalization: in the new basis $B$, the quadratic form looks like $\langle -1,1,4\rangle$. You have one negative coefficient, and two positive ones. So if you want your quadratic form to be positive on a subspace, you should take the subspace spanned by the basis vectors corresponding to the positive coefficients.

In your case, these are the second and third basis vectors, so $(-1,0.5,0)$ and $(2,1,1)$. And of course, if you take a vector in this subspace and write it in the new basis $B$, by construction it has a first component equal to $0$.

EDIT: I see the new answer states that the diagonalization itself is incorrect, which is indeed the case. I did not try to check that before answering. This being said, I leave my answer since it does provide the method to find the correct subspace (once you get the right diagonanization of course).

Captain Lama
  • 25,743
0

Your solution to the first part is incorrect. You cannot diagonalize a quadratic form by row-reducing the matrix. Two procedures are involved: "completing the square" and "forcing a non-zero diagonal." Your initial matrix has all zero terms on the diagonal so the first transformation is $$z=X+Z,y=Y,x=X$$ which gives $$2X^2+2ZX+2XY+4YZ$$ $$=2(X^2+XY+XZ)+4YZ$$ $$2((X+\frac{1}{2}Y+\frac{1}{2}Z)^2-\frac{1}{4}Y^2-\frac{1}{4}Z^2-\frac{1}{2}YZ)+4YZ$$ $$=2(X+\frac{1}{2}Y+\frac{1}{2}Z)^2-\frac{1}{2}Y^2-\frac{1}{2}Z^2+3YZ$$ The next transformation is $$X'=X+\frac{1}{2}Y+\frac{1}{2}Z,Y'=Y,Z'=Zi.e.$$ $$X=X'-\frac{1}{2}Y'-\frac{1}{2}Z',Y=Y',Z=Z'$$ so the quadratic form becomes $$2X'^2-\frac{1}{2}Y'^2-\frac{1}{2}Z'^2+3Y'Z'$$ $$=2X'^2-\frac{1}{2}(Y'^2-6Y'Z')-\frac{1}{2}Z'^2$$ $$=2X'^2-\frac{1}{2}((Y'-3Z')^2-9Z'^2)-\frac{1}{2}Z'^2$$ $$=2X'^2-\frac{1}{2}(Y'-3Z')^2+4Z'^2$$ Your final transformation is $$X''=X',Y''=Y'-3Z',Z''=Z',i.e.$$ $$X'=X'',Y'=Y''+3Z'',Z'=Z''$$ giving the quadratic form $$2X''^2-\frac{1}{2}Y''^2+4Z''^2.$$ By writing each of the transformations in matrix form and multiplying the matrices, you should have no problem finding a matrix $M$ such that $$\begin{bmatrix}x\\y\\z\end{bmatrix}=M\begin{bmatrix}X''\\Y''\\Z''\end{bmatrix}$$

P. Lawrence
  • 5,674
  • The solution for diagonalization is not mine. Those are the answers i got from our bank of exams. We use elementery cojgurence for getting the diagonalaized form in our book in the same way. Maybe they were wrong in the calculations but the way should be correct as far as what we studied. – Alon Apr 26 '20 at 08:17
  • That diagonalization wasn’t performed via simple row-reduction as you’ve assumed. It looks like some variation of reverse Hermite diagonalization was used. If you multiply things out, you’ll see that $M$ indeed diagonalizes the quadratic form. – amd Apr 26 '20 at 22:26
  • Anyway, this doesn’t address the actual question, which was about how to choose a subspace on which the form is positive-definite. I don’t see anything about that here. – amd Apr 26 '20 at 22:27
  • I deliberately refrained from saying anything about part (ii) because it seemed to me that part (i) was wrong and the OP was buiding on a weak foundaion, If I was wrong and reverse Hermite diagonalization was used, I apologize but the OP's statement "elementery cojgurence for getting the diagonalaized" makes me sceptiacal. My advice to the O.P. is first to learn some method of diagonalization by congruence , either reverse Hermite diagonalization or the method I outlined. After you unerstand the method and can do it yourself by hand, you can use a canned method,but not before. – P. Lawrence Apr 27 '20 at 01:44