I've been trying to do this for ages. I'm worried that it's impossible, but I have heard that it can be done by hand.
As long as I can get $x$ by hand I can obviously work out its value via calculator.
Please help, I am so stuck and desperately need assistance.
Thanks in advance!
First of all, that equation is highly nonlinear, as a result analytically we may not (can not) find a solution.
First Observation: Note that when $x$ becomes very large $e^{-x}$ becomes very small so $$e^{-x}-\sin x\approx0-\sin x$$ and hence the zeros of $\sin x$ are the zeros of $e^{-x}-\sin x$. This observation also ensures that solution for $e^{-x}-\sin x=0$ exists.
Second Observation: For $x<0$ $e^{-x}$ is an increasing function and dominates $\sin x$ (Which can be seen in the graph too) so there are no zeros of the function $e^{-x}-\sin x$ for $x<0$.
So what's the solution? Well, the solution can only be found by Numerical methods. One easy way to do that by plotting graphs.
This is the graph of $e^{-x}-\sin x$ where the first observation is visualized.
This is the graph showing the intersection of $e^{-x}$ [Blue line] and $\sin x$ [Red line].
In one word the solutions are $x=0.589,3.096,6.285$ etc.
Hope this works.
You cannot find a closed form for the zeroes, but you can find asymptotic approximations.
Let $x_n$ be the zero in $(\pi n-\frac \pi 2, \pi n+\frac \pi 2)$. Write $x_n=\pi n+\varepsilon_n$ with $|\varepsilon_n|<\frac \pi 2$.
Then $$e^{-\pi n -\varepsilon_n}=\sin(\pi n+\varepsilon_n)=(-1)^n\sin(\varepsilon_n)\tag{1}$$ Taking the limit, the left-hand-side converges to $0$. So this implies that $\varepsilon_n\rightarrow 0$. Thus, using Taylor expansions in $(1)$, $$e^{-\pi n}(1+o(1))= (-1)^n \varepsilon_n(1 +o(1))$$ which means that $$\varepsilon_n=(-1)^ne^{-\pi n}(1+o(1))$$
$$\boxed{x_n=\pi n+(-1)^n e^{-\pi n} + o(e^{-\pi n})}$$ The zeroes therefore converge exponentially fast towards multiples of $\pi$.
You can keep playing that game and plug the residual back into $(1)$ to find the next term in the expression of $x_n$, but this is already converging quite fast.
If you build the series expansion of the rhs of $$y=e^{-x}-\sin(x)$$ around $x=n \pi$ and later series reversion forcing $y=0$, you obtain $$x_n=n\pi+\frac{1}{1+e^{(1+i) \pi n}}+\frac{1}{2 \left(1+e^{(1+i) \pi n}\right)^3}+\cdots$$
$$\left( \begin{array}{ccc} n & \text{approximation} & \text{solution} \\ 0 & 0.5625000000000000000 & 0.5885327439818610774 \\ 1 & 3.0963808805403588820 & 3.0963639324106461156 \\ 2 & 6.2850492723072431593 & 6.2850492733825865338 \\ 3 & 9.4246972547386088459 & 9.4246972547385212191 \\ 4 & 12.566374101689367670 & 12.566374101689367677 \\ 5 & 15.707963117247215942 & 15.707963117247215942 \\ 6 & 18.849555928051171524 & 18.849555928051171524 \\ 7 & 21.991148574847125823 & 21.991148574847125823 \\ 8 & 25.132741228730507464 & 25.132741228730507464 \\ 9 & 28.274333882307613598 & 28.274333882307613598 \\ 10 & 31.415926535897955096 & 31.415926535897955096 \end{array} \right)$$
Although there are already a few answers, all complex roots, except for $z=0.5885327\dots$ discussed here, have a simple explicit series expansion. For the real roots, substitute $w=e^{2iz}\iff z=\pi k-\frac i2\ln(w)$, apply Lagrange reversion, and use factorial power $n^{(m)}$: $$e^{-z}=\sin(z)\iff w=1+2ie^{(i-1)\pi k}w^\frac{1+i}2\implies z_k=\pi k-\frac i2\left(\ln(1)+\sum_{n=1}^\infty\frac{(2 ie^{(i-1)\pi k})^n}{n!}\left.\frac{d^{n-1}}{dw^{n-1}}\ln’(w)w^{\frac{1+i}2n}\right|_1\right)=\pi k+\sum_{n=1}^\infty \frac{(2i)^{n-1}(-e^{-\pi})^{ k n}}{n!}\left(\frac{1+i}2n-1\right)^{n-1}$$ There are two sets of complex roots which are conjugates of one another. To find them, substitute $u=e^{(1\pm i)z}\iff z=\frac{2\pi i k}{1\pm i}+\frac{\ln(w)}{1\pm i}$ and use Lagrange reversion: $$e^{-z}=\sin(z)\iff w=\pm2i+e^{2\pi k}w^{\pm i}\implies z_k=\frac{2\pi ik}{1\pm i}+\frac1{1\pm i}\left(\ln(\pm 2i)+\sum_{n=1}^\infty \frac{e^{2\pi kn}}{n!}\left.\frac{d^{n-1}}{dw^{n-1}}\ln’(w)w^{\mp in}\right|_{\pm2i}\right)=\frac{1\pm i}4((4k\mp1)\pi i+2\ln(2))+(1\pm i)\sum_{n=1}^\infty \frac{(\mp 2i)^{(-1\pm i)n}e^{2\pi k n}}{2n!}(\pm in-1)^{(n-1)}$$
For the real roots, $k\in\Bbb N$ and $\pm k\in\Bbb N$, for the complex roots, depends on whether all top/bottom signs are taken. The location of the $-z$ roots is described here. Therefore:
$$\bbox[3px,border: darkturquoise 3px solid]{e^{-z}=\sin(z)\implies z_k= \pi k+\sum_{n=1}^\infty \frac{(2i)^{n-1}(-e^{-\pi})^{ k n}}{n!}\left(\frac{1+i}2n-1\right)^{n-1},z_{\pm k}= \pm\frac{1\pm i}4((4k-1)\pi i+2\ln(2))+(1\pm i)\sum_{n=1}^\infty \frac{(\mp 2i)^{(-1\pm i)n}e^{\mp2\pi k n}}{2n!}(\pm in-1)^{(n-1)};k\in\Bbb N}$$
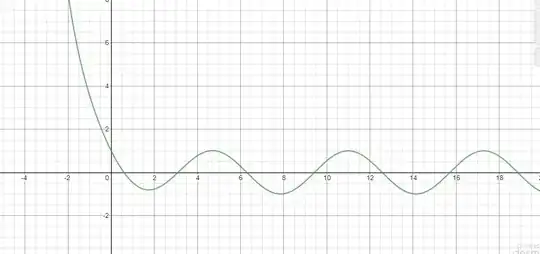
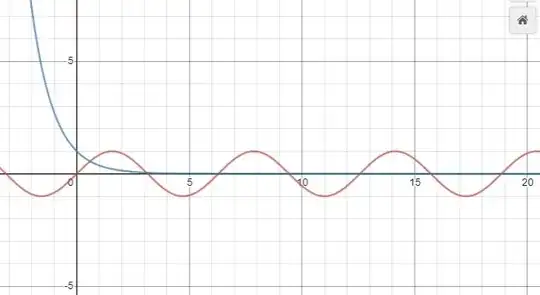
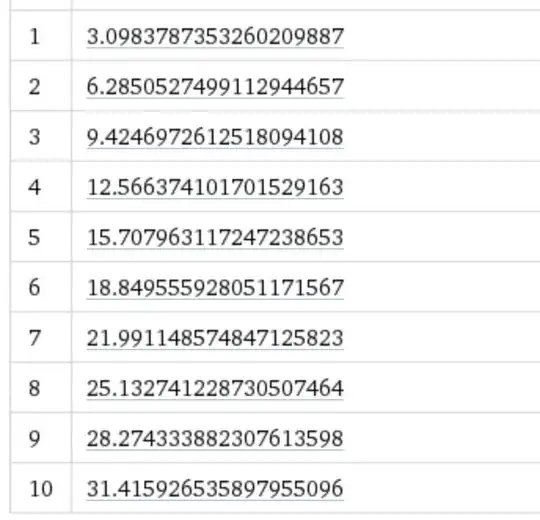
The real roots are shown here, rounded matching @Claude Leibovici’s, and the complex roots are shown here. If $n=0$, the series diverges so the Fox Wright function cannot easily be used. Also, if all of its parameters were extended to complex numbers and the $n=0$ problem were gone, then Fox Wright would give a closed form. Also, unless all parameters were extended into being complex, this function does give a closed form as well. It is of interest to find a similar expansion for $z_0= 0.5885327\dots$
