I want to construct a map from the g-Torus $T^g$ to a wedge of g tori $T^1\vee···\vee T^1$ which induces an isomorphism on $H^1(T^1\vee···\vee T^1)\to H^1(T^g)$.
According to Hatcher, the map is
Is there a formal definition? How does it work on the generators of $H^2(T^1\vee...\vee T^1)$?
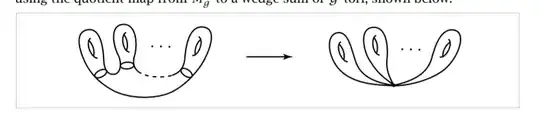
Here is a more formal construction:
Let $D_1,\dots, D_g$ be disjoint closed embedded disks in $S^2$, and let $S = S^2 \setminus (\sqcup_i int(D_i))$. Let $H = T^1 \setminus D$ for some closed embedded disk, and for each $i$ choose a homeomorphism $f_i\colon \partial H \stackrel{\cong}{\to} \partial D_i$. Then we can construct the genus $g$ surface as
$$ T^g \cong S \sqcup_{\{f_i\}} (\sqcup_{i=1}^g H). $$ In English, attach $g$ handles to the $2$-sphere. Then the quotient $T^g / S$ is homeomorphic to $\vee_{i=1}^g T^1$.
Now since $(T^g, S)$ is a "good pair" in the sense of Hatcher, you can use the fact that $\tilde{H}^*(T^g/S)\cong H^*(T^g, S)$ to prove that the quotient map induces an isomorphism on $H^1$ using the long exact sequence of the pair. Here's what the l.e.s. looks like at the bottom:
$$0 \to H^0(T^g) \stackrel{\cong}{\to} H^0(S) \to H^1(T^g, S) \to H^1(T^g) \to H^1(S) \to H^2(T^g, S) \to H^2(T^g) \to 0 $$ so if we start at $H^1(T^g,S)$ and plug in known values we get
$$ \mathbb{Z}^{2g} \to\mathbb{Z}^{2g} \to \mathbb{Z}^{g-1} \to \mathbb{Z}^g \to \mathbb{Z}$$
Here we've used the facts that $H^*(T^g, S) \cong \tilde{H}^*(\vee_{i=1}^g T^1)$ and $S \simeq \vee_{i=1}^{g-1} S^1$. Now, the first two groups are isomorphic, but we need to know that the map between them is actually an isomorphism and not just injective onto some proper subgroup. Consider the last three groups: the last map surjects onto $\mathbb{Z}$ and its kernel is isomorphic to $\mathbb{Z}^{g-1}$; the group $\mathbb{Z}^{g-1}$ surjects onto this kernel, and since they are both free with the same rank this map must be injective as well. Therefore the last three groups form a short exact sequence, so the first map must be an isomorphism.
To get an explicit description of $H^2(q)$, it will suffice to know the cup product structure for $T^g$ (see for example here and here). When $g=1$, $H^*(T^1)$ has elements $\alpha, \beta$ which generate $H^1(T^1)\cong\mathbb{Z}^2$ as a group, and $\alpha \cup \beta$ generates $H^2(T^1)\cong \mathbb{Z}$. For higher $g$, there are pairs $\alpha_1, \beta_1,\dots,\alpha_g, \beta_g$ which together generate the group $H^1(T^g)\cong \mathbb{Z}^{2g}$, the product $\alpha_i \cup \beta_i$ generates $H^2(T^g)\cong \mathbb{Z}$ for any $i$, and the products $\alpha_i^2$ and $\alpha_i\cup \beta_j$ for $i\neq j$ are all $0$. In particular $\alpha_i\cup \beta_i = \alpha_j\cup \beta_j$ for any $i,j$.
Now consider $W = \vee_{i=1}^g T^1$: let $a_i, b_i$ be the generators of $H^1$ of the $i$-th copy of $T^1$, so their product generates $H^2$ of the $i$-th copy of $T^1$. Then $q^*(a_i) = \alpha_i$ and $q^*(b_i) = \beta_i$, and since $q^*$ is a ring homomorphism we get $ q^*(a_i \cup b_i) = \alpha_i \cup \beta_i = 1 \in H^2(T^g) $. Then if $c = \sum_{i=1}^g c_i (a_i \cup b_i)$ is an arbitrary element of $H^2(W)\cong \mathbb{Z}^g$, we have
$$q^*(c) = q^*(\sum_{i=1}^g c_i (a_i \cup b_i)) = \sum_{i=1}^g c_i \alpha_i \cup \beta_i = \sum_{i=1}^g c_i $$
