Deducing the effect of a map on homology by its effect on local homology groups.

Question

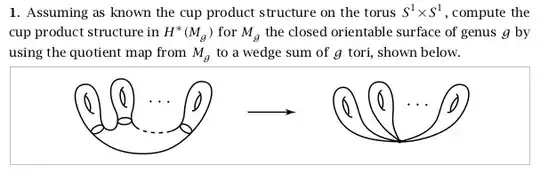
I'm working through the following exercise in hatcher. I would like to know how this map acts on the cohomology groups before computing the cup product. I denote the wedge sum of $g$ tori by $N$.

My main confusions are 1) in the first part how do we deduce that $c$ is mapped to the sum of $c_i$ by some local argument, and 2) how do we rigorously see that the generators are indeed mapped to where they should be.

How does this map act on the second cohomology groups

$H_2(M_g)$ has one generator which we denote $\sigma$. $H_2(N)$ has $g$ generators $\sigma_i$ one for each torus in the wedge. Intuitively $\sigma$ should be mapped to the sum of the $\sigma_i$ (maybe this should have alternating signs). I have found an argument here that I do not quite understand. Here is an extract of the argument

I do not understand how the above argument deduces that $\sigma$ is mapped to the sum. A generator of $H^2(M_g,M_g-x)$ is sent to a generator of $H^2(N,N-q(x))$, but how does a sum come into play?

How does this map act on the first cohomology groups

Intuitively this map should be an isomorphism. Reducing the middle trivial space to a point does not affect the loops which are the generators of $H_1(M_g)$, and it maps each generator in $M_g$ to a corresponding generator in $H_1(q(M_g))$. I am not sure how to make this rigorous.

Answer 1

You are mixing up $H^*$ and $H_*$ a lot in your question, so it's not clear if you want to know about homology, cohomology, or both. Since the question title and the argument you're trying to understand are using homology, I will focus on that.

The argument you pasted has a significant error: the map $H_2(\vee_g T) \to H_2(\vee_g T, \vee_g T - q(x))$ is not an isomorphism if $g > 1$, it is the projection map $\mathbb{Z}^g \to \mathbb{Z}$ onto the factor corresponding to the torus containing $q(x)$ (you can still see this from the long exact sequence of the pair).

Since $q_*(c) \in H_2(\vee_g T)$, we know it is equal to $\sum_{i=1}^g a_i c_i$ for some coefficients $a_i \in \mathbb{Z}$. For a fixed $i$, choose an $x \in M_g$ such that $q(x)$ is not the basepoint and is contained in the $i$-th copy of $T$. Then from the true parts of the argument you pasted, the class $q_*(c)$ maps to the same element in the relative homology group as $c_i$ (up to sign, but we can chose generators so the sign is always $+$), and since the vertical map is projection onto the $i$-th coordinate that means that the coefficient of $c_i$ in $q_*(c)$ is $1$. Since this holds for each $i$, $q_*(c) = \sum c_i$.

The map $q_*\colon H_1(M_g) \to H_1(\vee_g T)$ is indeed an isomorphism, and you can see it from the long exact sequence for the pair $(M_g, S)$, where $S \sim \vee_{g-1} S^1$ is the subspace that Hatcher quotients out. You will see that $q_*$ is surjective, so since they are both free abelian groups with the same rank it must be an isomorphism.

---

The argument for cohomology is very similar, and you would want to use the same diagram as for homology but with all the arrows reversed. Now you have a map $q^*\colon H^2(\vee_g T) \to H^2(M_g)$, and the statement you're trying to prove is $(a_1,\dots, a_g) \mapsto \sum_i a_i$. For this you just need to show $q^*(\kappa_i) = \kappa$, where $\kappa_i$ generates $H^2$ of the $i$-th copy of $T$ and $\kappa$ generates $H^2(M_g)$.