This is a exercise that I came across while studying a geometry textbook.
Use the method of induction to prove the area formula of a rectangle whose two sides are natural numbers.
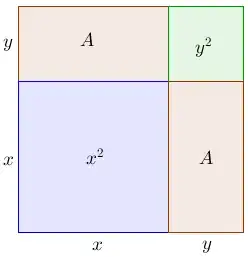
I can derive the simple formula of the area of a rectangle by using a method like this:
And so we can derive that $A = xy$ by using $x^2 + y^2 + 2A = (x + y)^2$.
However, I'm having some trouble using induction to prove this. How should I start this problem? Any tips are welcome, thanks.