How to embed the " epsilon / delta" definition of a limit in a formal proof in natural deduction style with quantifiers?

Question

• In order to grasp a notion better, it find useful to make use if it in formally rigorous reasonings. This is somewhat artificial and is not practiced by those who are familiar with the concepts, but that is the way my mind works.

Currently, I try to understand the " epsilon / delta" definition of the limit of a function at some value a.

I would like to imbedd the definition in a formal reasoning, applying natural deduction rules.

• I am not talking about he global structure of the proof which is clear to me :

Premise (1) [L is the limit ....] IFF [ for all epsilon.., there is a delta...]

Premise (2) It is the case that [ for all epsilon.., there is a delta...]

Conclusion (3) Therefore [L is the limit ....]

I mean, the logic of the " iff" elimitating is clear enough.

• My question deals with the proof of premise 2 ( in the above argument).

More precisely, my main problem is this : in the proof of premise (2) how to introduce the existential quantifer?

I feel uncomfortable with the examples I have seen so far, when teachers do not introduce explicitly the quantifier " there is some delta such that" and simply say " set delta equal to ..." . What I mean is : is setting a variable at some value the same as introducing an existential quantifier.

To put it another way : in the examples I have seen, the fact that the proof is an existence proof is not made clear enough to me. The existence of the " delta" seems to be postulated rather than proved.

Another problem : if the existence of "epsilon" is not supposed , how could defining "epsilon" in terms of delta could amount to proving the existence of "epsilon"? However, " epsilon" is quantified universalllly, not existentially.

Sure I am missing something here, but can't find out what.

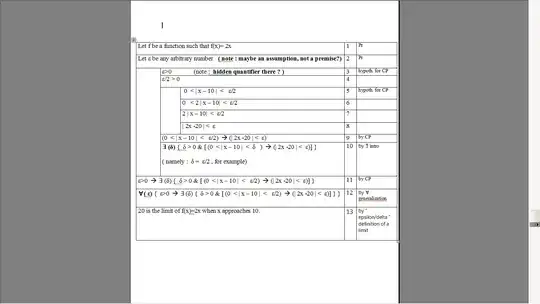
• So, would it be correct to proceed as follows to formalize the example given by the excellent Jim Fowler ( Ohio State Uni.) in his " Calculus Mooculus Week 2 Lecture 14 " video ? ( https://www.youtube.com/watch?v=-9HyfES1VB0&list=PLaLOVNqqD-2H1OJRzQDqYjGjM-XeJCALw&index=28)

The goal is to prove that : "lim ( as x --> 10) of f(x)=2x is 20" .

Answer 1

Actually it seems that your question has not been really answered yet.

The true formal structure of the proof would look like this:

~ ~ ~

Given any $ε{∈}\mathbb{R}_{>0}$:
  $\vdots$
  $∃δ{∈}\mathbb{R}_{>0}\ ( \cdots )$.
$∀ε{∈}\mathbb{R}_{>0}\ ∃δ{∈}\mathbb{R}_{>0}\ ( \cdots )$.

~ ~ ~

Now the question is how to prove the existential. For this you must look closely at the rules of the formal system you are working in. For example, take this Fitch-style natural deduction system. The ∃-intro rule allows us to introduce the existential quantifier. In many simple limit problems, the formal proof in this system would look like:

~ ~ ~

Given any $ε{∈}\mathbb{R}_{>0}$:
  $\vdots$
  Let $d∈\mathbb{R}$ such that ...
  $\vdots$
  $d > 0$.
  Given any $∀x∈\mathbb{R}$:
    If $|x-c|<d$:
      $\vdots$
      $|f(x)-L|<ε$.
  $∀x∈\mathbb{R}\ ( |x-c|<d ⇒ |f(x)-L|<ε )$.
  $∃δ{∈}\mathbb{R}_{>0}\ ∀x∈\mathbb{R}\ ( |x-c|<δ ⇒ |f(x)-L|<ε )$.   [by ∃-intro]
$∀ε{∈}\mathbb{R}_{>0}\ ∃δ{∈}\mathbb{R}_{>0}\ ( \cdots )$.

~ ~ ~

Note that in the system I linked to, the "Let $d∈\mathbb{R}$ ..." can only be done via the ∃-elim rule. For example, if you "let $d = ε/2$" you are actually using "$∃d{∈}\mathbb{R}\ ( d = ε/2 )$". As you can see, for simple cases like this it is trivial, because this can be obtained from "$ε/2 = ε/2$" by ∃-intro. But for more complicated examples, you may not be able to directly construct $d$ and can merely prove that some real $d$ exists with the properties you want, in which case it really becomes important to understand the role of ∃-elim.

For example, to prove the limit sum property, namely if $\lim_{x→c} f(x) = L$ and $\lim_{x→c} g(x) = M$ then $\lim_{x→c} (f(x)+g(x)) = L+M$, you need to do the following:

~ ~ ~

Given any $ε{∈}\mathbb{R}_{>0}$:
  $ε/2∈\mathbb{R}_{>0}$.
  Thus $∃δ{∈}\mathbb{R}_{>0}\ ∀x∈\mathbb{R}\ ( |x-c|<δ ⇒ |f(x)-L|<ε/2 )$.
  And $∃δ{∈}\mathbb{R}_{>0}\ ∀x∈\mathbb{R}\ ( |x-c|<δ ⇒ |g(x)-M|<ε/2 )$.
  Let $d_1∈\mathbb{R}_{>0}$ such that $∀x∈\mathbb{R}\ ( |x-c|<d_1 ⇒ |f(x)-L|<ε/2 )$.
  Let $d_2∈\mathbb{R}_{>0}$ such that $∀x∈\mathbb{R}\ ( |x-c|<d_2 ⇒ |g(x)-M|<ε/2 )$.
  Let $d = \min(d_1,d_2)$.
  Then $d∈\mathbb{R}_{>0}$.
  Given any $∀x∈\mathbb{R}$:
    If $|x-c|<d$:
      $|x-c|<d_1$.
      $|x-c|<d_2$.
      $|f(x)-L|<ε/2$.
      $|g(x)-M|<ε/2$.
      $\vdots$
      $|(f(x)+g(x))-(L+M)|<ε$.
  $\vdots$
  $∃δ{∈}\mathbb{R}_{>0}\ ∀x∈\mathbb{R}\ ( |x-c|<δ ⇒ |(f(x)+g(x))-(L+M)|<ε )$.

Answer 2

Consider the statement

For every positive integer $n$ except $1$ there exists a prime $p$ such that $p$ divides $n$.

Does it bother you in the same manner as the definition of limit? I guess not.

The complexity of definition of limit arises not because of quantifiers but is more related to the part after "such that". The statement above has a much simpler condition to check about divisibility. The limit definition has a complicated check which involves another universal quantifier:

such that for every $x$ with $0<|x-a|<\delta$ we have $|f(x) - L|<\epsilon$.

Compare this with the far simpler statement

For every $\epsilon>0$ there exists a $\delta >0$ such that $\delta<\epsilon $.

Also you should see the proof of the number theoretic statement given at the start of this answer. The proof is existential as it does not give $p$ explicitly in terms of $n$ nor indicate a simple procedure to find $p$ given $n$.

The typical $\epsilon, \delta$ proofs on the other hand try to find explicit expressions for $\delta$ in terms of $\epsilon$. Here some authors don't do a decent job (the image in your question as well as this question).

The typical $\epsilon, \delta$ proof should begin by analysis of the target inequality $|f(x) - L|<\epsilon$ view a view to simplify it so much so that the existence of $\delta$ which ensures this inequality is obvious.

---

You should also try to understand the negation of limit definition because it reverses the quantifiers. For example you can try to prove that $\lim_{x\to 2}x^2\neq 5$.