Introduction:
So this ties a lot into how we define many "infinite processes." Some of the more familiar ones are these:
$$\sum_{k=0}^\infty x^k = \frac{1}{1-x} \; \text{whenever} \; |x| <1$$
- Infinite products, such as
$$\prod_{p \; prime} \frac{1}{1-p^{-2}} = \frac{\pi^2}{6}$$
- Infinitely-nested radicals, such as
$$\sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+\cdots}}}}=3$$
- And, of course, continued (infinite) fractions as well...
Defining Infinite Processes: Convergents:
Basically, we find a "convergent" of sorts - a "partial" and finite version of the infinite thing - and find the limit as we take infinitely many. What might these convergents look like? Usually, it depends on the context. For instance, for sums and products, we just take finitely many terms. For radicals and fractions, we truncate the expression and find the limit as we truncate further down the line.
Thus, for instance,
$$\sum_{k=0}^\infty x^k = \lim_{n \to \infty} \sum_{k=0}^n x^k \;\;\;\;\; \text{and} \;\;\;\;\; \prod_{p \; prime} \frac{1}{1-p^{-2}} = \lim_{n \to \infty} \prod_{\text{the first n primes}} \frac{1}{1-p^{-2}}$$
For radicals and fractions, it's easier to think of them in terms of a sequence, in which we continue adding one more term at each step. For instance, for the radical expression above,
$$\sqrt 1 \;\;\; , \;\;\; \sqrt{1 + \sqrt 2} \;\;\; , \;\;\; \sqrt{1 + \sqrt{2 + \sqrt 3}} \;\;\; , \;\;\; \sqrt{1 + \sqrt{2 + \sqrt{3 + \sqrt 4}}} \;\;\; , \;\;\; \cdots$$
...in which the obvious pattern holds to get the infinite radical from before, is a sequence which approaches $3$.
Similarly, for an infinite nested fraction, we can truncate before each plus or minus sign:
$$1 \;\;\; , \;\;\; 1 + \frac 1 1 \;\;\; , \;\;\; 1 + \frac{1}{1 + \frac 1 1} \;\;\; , \;\;\; 1 + \frac{1}{1 + \frac{1}{1 + \frac 1 1}} \;\;\; , \;\;\; \cdots$$
will be the sequence of convergents for your infinitely nested fraction. In light of this, it is clear that your sequence is always positive. You have logically assigned a value for your sequence as well (albeit on the premise that it converges in the first place).
In that light, there is only one value which this expression could reasonably have: $\varphi$, or $(1+ \sqrt 5)/2$. The negative solution won't work!
Summary & Connections:
In short, for infinite processes such as these, we like to define a series of convergents by truncating the infinite operation or expression or whatever at finite places, each further down the line. Then we consider the limit of these truncated expressions as we go further and further down the line. This is much akin to how, in calculus, we define an infinite sum as the limit of the partial sums, but more generally!
This method, provided the limit exists of course, allows us to properly assign a value to a given infinite expression. Sometimes other methods like yours will result in that value being vague - you get a multiplicity of values, but you can't be sure which value is "right," much akin to how certain methods of equation solving introduce extraneous solutions. However, this method allows us to, if nothing else, verify which of that plurality is correct!
A Note On Stability:
There is one more topic I'd like to touch on: stability of solutions to an iterative process. As you might be able to guess from the sequence of convergents for your infinite fraction, we can devise a recurrence relation that describes how to get the next convergent from the previous:
$$a_{n+1} = 1 + \frac{1}{a_{n}}$$
Dynamical systems and a lot of application-related things also have stability as a core concept. So it is true here.
Of course, as you might imagine, we want to consider the limit $\lim_{n \to \infty} a_n$ - that would be your infinite fraction again, no? But there's an issue: what is our first term of the sequence? Our initial condition of the recurrence?
Here's where things get really interesting, and why your negative solution is not something to be thrown away carelessly...
Start by defining, say, $a_1 = 1$. Playing around in Excel, then, we get this:
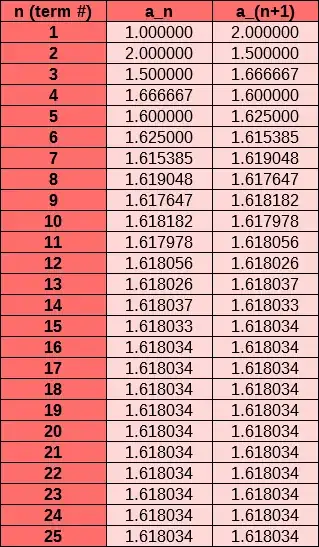
Let's play around with other initial values. Here's a few samples: $a_1=2,\pi,1000$.
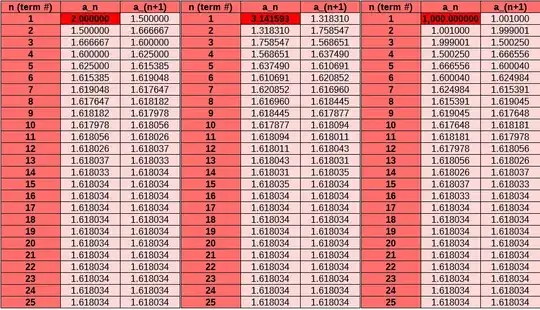
Notice something? Each sequence converges (quite quickly) to $1.618$ or so. That is, it converges to the golden ratio, $(1+\sqrt 5)/2$.
In fact, let's even get close to the negative solution. We call this the conjugate of the golden ratio, $\bar \varphi = (1-\sqrt 5)/2 \approx -0.618.$ Playing around in Excel some more, let's set $a_1=-0.9,-0.618,$ and $-0.618034$, increasingly close approximations to $\bar \varphi$.
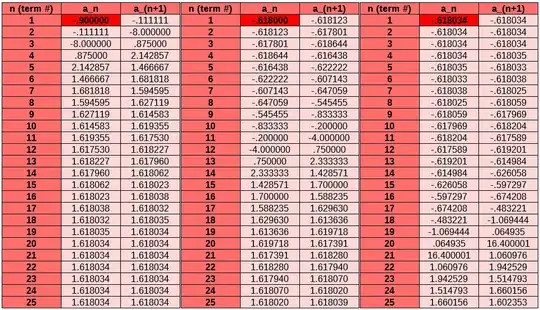
But I wonder... What if $a_1 = \bar \varphi$? Let's try that!
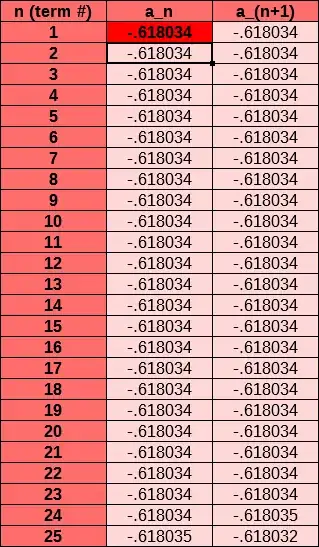
What we notice is quite incredible: even after comparatively many iterations, $a_n \approx \bar \varphi$ even still! In fact, the divergence itself is only a result of computer error - truncated decimals, rounding and approximation errors, and so on! If you do the math by hand, you'll find that if $a_1 = \bar \varphi$, so does $a_2$. And $a_3.$ And $a_4$. And so on.
This touches on the notion of stability. Let's summarize our observations.
Whenever $a_1 \ne \bar \varphi$, $a_n$ approaches $\varphi$. It might take a while, but no matter how large or small or negative or close to $\bar \varphi$, it eventually approaches it. (Unless we run into a divide-by-zero error along the way but that's just something to ignore.)
Whenever and only whenever $a_1 = \bar \varphi$, $a_n$ does not approach $\varphi$ but rather it stays at $\bar \varphi$.
In such a case, we call $\varphi$ a "stable" solution because (within some amount of reason, since some systems will have multiple stable/unstable solutions) assigning $a_1$ a value near $\varphi$ (or anywhere aside the unstable solution in this case) will ensure $a_n \to \varphi$.
On the other hand, $\bar \varphi$ is an "unstable" solution, because even if you start near it, $a_n$ eventually goes away from it, towards $\varphi$ in this case. However, if $a_1 = \bar \varphi$, then $a_n \to \bar \varphi$.
So while your fraction might only have $\varphi$ as a reasonable way of assigning its value, $\bar \varphi$ has an interesting role to play with respect to stability.



