1

Why do we take thickness be differential of distance apart of elemental mass when calculating volume and be differential length of arc when calculating area of the sphere when integrating in terms of angle.

sphere elemental part

Before going into depth I refer this thread first.

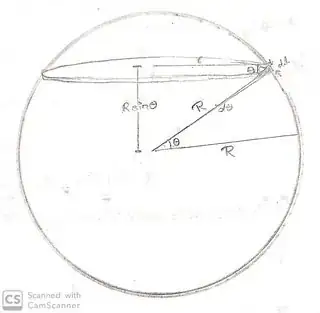
So what I learnt is that when getting small volume we take $$dl = d(R\sin θ) = R\cos θ\cdot dθ <<$$ $$r = R\cosθ$$ $$dV = πr^2\cdot dl$$

While when calculating area we take $dl$, $$dθ = \frac{dl}{R}$$ $$dl = R\cdot dθ <<$$ $$dA = 2πr\cdot dl$$

But like why different elemental thickness ($dl$) for those calculations?

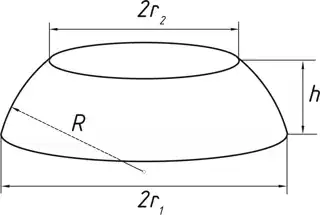
If I wasn't able to make you understand what I said, then see the second figure, the $h$ is taken as $dl$ in calculation of volume while the curved-surface is used as $dl$ for calculation of area

My Question is: WHY

emacs drives me nuts
  • 10,390
  • 2
  • 12
  • 31
Animesh Sahu
  • 193

2 Answers2

1

Think of these computations as bases on the piling of cone frustra.

The volume of a single frustrum is the base area by the height, $\pi r^2\,dh$.

The lateral area is the circumference of the base times the slant height, $2\pi r\dfrac{dh}{\cos\theta}$.

(For thin frustra, the difference between the two bases does not matter.)

  • I am confused towards the volume calculation, why didn't we took the curved surface (slant height) ? If we take frustum's height, we are missing very small volumes, aren't we? – Animesh Sahu Feb 14 '20 at 14:55
  • @AnimeshSahu: by analogy, when computing the area of a right trapezoid, will you take the height or the oblique side length ? –  Feb 14 '20 at 15:00
  • 1
    Ohh right, gotcha will take perpendicular height. – Animesh Sahu Feb 14 '20 at 15:11
0

This is because $\theta \to 0$ so $$ \frac{d \sin \theta}{d\theta}=\lim_{\theta \to 0}\frac{\sin \theta}{\theta}=1 $$ In other words if $\theta$ is small the difference with $\sin \theta$ is much more small.

Emilio Novati
  • 62,675
  • But question remains the same why do we take different elemental length for the elemental thickness? – Animesh Sahu Feb 14 '20 at 14:52
  • Because for the surface we need an arc along the surface and for the volume the height of the disc. – Emilio Novati Feb 14 '20 at 14:54
  • why didn't we took the curved surface (slant height) in volume calculation? If we take height of disc, we are missing very small volumes or taking very small excess volume, aren't we? – Animesh Sahu Feb 14 '20 at 14:57
  • My answer explain exactly why, for $\theta \to 0$ the curved arc and the height are ''the same'', so the the ''very small excess volume'' goes also to $0$ – Emilio Novati Feb 14 '20 at 15:01
  • But if we take height of disc, https://i.imgur.com/zqo3ZsQ.jpg this much volume is excess right, but if you take slant height then check the post linked in the question it gives $\frac{π^2r^3}{2}$ as volume which is wrong right? – Animesh Sahu Feb 14 '20 at 15:06