3

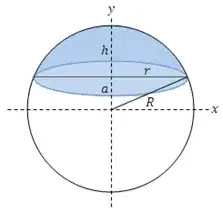
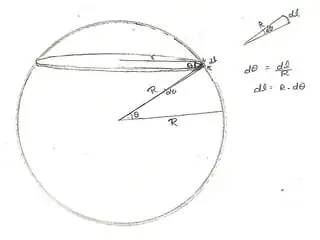
As far as I dig into higher mathematics, I found a problem myself for getting volume of a spherical cap, as I was doing some experiments with Archimedes Principle.

spherical capspherical cap handwritten

So what I did was take elemental mass in terms of angle θ taking center of sphere as origin.

So, lets see what I did and what i was getting

$$r = R\cos θ$$ (vertically-opposite angle, see Z looking in figure)

Now volume of small elemental mass $$dV = πr^2\, dl$$ (where $dl$ is thickness) $$dl = R\,dθ$$ Putting all together $$dV = π(R\cos θ)^2(R\,dθ)$$ $$dV = πR^3\cos^2θ\,dθ$$

Now total volume of the sphere if i want to calculate to check this formula is working correct, $$V = \int_{-π/2}^{π/2} πR^3 \cos^2θ\,dθ$$ $$V = πR^3 \int_{-π/2}^{π/2} \cos^2θ\,dθ$$ $$V = πR^3 \int_{-π/2}^{π/2} \frac{1+\cos2θ}{2}\,dθ$$ $$V = πR^3 \left[ \frac{θ}{2} + \frac{\sin 2θ}{4} \right]_{-π/2}^{π/2}$$ $$V = \frac{π^2R^3}{2}$$

But this contradicts the fact that Volume of sphere is $\frac{4}{3}πR^3$

And in fact, the surface area of the sphere is taken out of this method to, instead taking $πr^2\,dl$ we use $2πr\,dl$ to get elemental area and then integrate from 0 to $\frac{π}{2}$ and then twice that. But doing that will not gonna help in getting volume of a spherical cap, so I took elemental volume.

What is done wrong in this method, any help would be appreciated. :)

emacs drives me nuts
  • 10,390
  • 2
  • 12
  • 31
Animesh Sahu
  • 193
  • How did you get a $\pi^2$ in your last step? At that stage I'd think you were plugging in $\pi/2$ into $\theta/2$ at endpoints... Something still off though, cn't see how the division by 3 would come up. – coffeemath Feb 14 '20 at 11:32
  • @coffeemath when you plug either of $\frac{π}{2}$ or $-\frac{π}{2}$ sin2θ vanishes, when you put limits in $\frac{θ}{2}$ it becomes $\frac{π}{4}+\frac{π}{4}$ which indeed is $\frac{π}{2}$ which when multiplied by $πR3$ becomes $\frac{π^2R^3}{2}$ – Animesh Sahu Feb 14 '20 at 11:39

2 Answers2

3

Yes, $r=R \cos \theta$ is OK. But also $z=R \sin \theta$ so $dz=R \cos \theta d \theta.$ Then you end up integrating $\pi (R \cos \theta)^2 \cdot (R \cos \theta d \theta)$ i.e. $\pi R^3 (\cos \theta)^3,$ and the cube of cosine integrates to $4/3$ when done $-\pi/2$ to $\pi/2.$

coffeemath
  • 7,403
  • What is z in this context? Any image? – Animesh Sahu Feb 14 '20 at 12:31
  • Even if i didnt understand about z, This still doesn't show similarity with the second last paragraph of the question. It contradicts if i understand correctly. – Animesh Sahu Feb 14 '20 at 12:35
  • 1
    $z$ is the $z$ axis going perpendicular to the equator of the sphere. And then $dz$ is the thickness of the disc you have of radius $r.$ – coffeemath Feb 14 '20 at 12:46
  • So upvote for that, but i still didn't understand why does z=Rsinθ,what i understand is that this length is Rsinθ https://imgur.com/a/Xz9rYyp before accepting the answer please let me understand that logic. – Animesh Sahu Feb 14 '20 at 13:01
  • What is $z = Rsinθ$ diagramatically, can you send a diagrammatic image? – Animesh Sahu Feb 14 '20 at 13:10
  • Ohh so i understand this part, but what about last second paragraph, could you also provide some info for why does this logic doesn't work for calculating the surface area of the sphere, like hell yea we use dl=R.dθ there, but why thickness there is different from thickness right here? – Animesh Sahu Feb 14 '20 at 13:28
  • Your diagram on imgur.com of what $z$ is looks right to me. It goes upward along $z$ axis, and has length $R \sin \theta$ using trig. I don't know how to put diagrams here but as I say yours already looks right. Then $dz=R \cos \theta d\theta$ is the differential of $z$ used for thickness. – coffeemath Feb 14 '20 at 13:31
  • I didn't really follow your reasoning so I just went "back to basics" and got thickness dz only after getting z. – coffeemath Feb 14 '20 at 13:34
1

You have a mistake in determining the thickness. By looking at this picture, you can see that the thickess $h$ isn't the same as the length of an arc $Rd\theta$, and you need an additional factor of $\cos\theta$, which makes your integral equal to $\frac43\pi R^3$ as it should be.

enter image description here

Community
  • 1
Vasily Mitch
  • 10,129
  • Yeah, it does make it equal to $\frac{4}{3}πR^3$ but I didn't understood why did we take additional factor of $cosθ$, can you explain a bit more? :) – Animesh Sahu Feb 14 '20 at 12:09
  • And also why does the second last paragraph of question works?, why don't we need additional factor of $cosθ$ over there? – Animesh Sahu Feb 14 '20 at 12:14