3

Like many of the best problems I found this one on twitter.

"In a square with side length 1, two random points in the square are connected by segments to two opposite vertices. How likely is it that the two segments will intersect?"

Diagram of a square with 100 pairs of random points selected, connected and the intersections noted as white circles. There are 6 intersections in this trial.

Steve Phelps, who posted this problem, uses desmos to solve it by experimentation. Here is his notebook.

He gets a very low probability about of about .09. But, I'd like the algebraic result.

I've reduced the problem to the following:

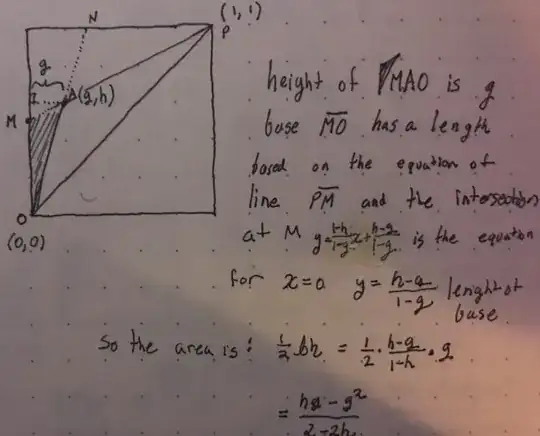
Diagram on notebook paper of a 1x1 square and the triangular region where point B must be place for an intersection with the line segment connected to A to occur. (given both points are on the same side of the diagonal connecting the vertices of the square connected to points A and B.)

WLOG we can consider the case where both of the randomly chosen points are on the same side of the diagonal formed by connecting the vertices we will connect to the random points. If we consider a random point A, then BP will intersect AO if B is in the shaded region.

What is the average area for that region if we pick a random point?

I did some snooping and random point picking can be a rich problem.

Maybe Steve had the right idea going with an experiment.

Still I'd like to work this out. I think I can use this formula:

Screen cap of formula on the page: http://mathworld.wolfram.com/TriangleTrianglePicking.html

With vertices: (0,0), (1,0), (0,1)

I don't know how to fix the vertices of the randomly picked triangle at $\left(0, \frac{h-g}{1-g}\right)$, (0,0) and (h,g) using this formula. So, maybe another approach is needed?

futurebird
  • 6,248
  • Just setup an integral, the answer is $1/12$. – Lee David Chung Lin Feb 03 '20 at 12:35
  • 1
    BTW, here the vertices are diagonal, and in this related post the vertices are adjacent. – Lee David Chung Lin Feb 03 '20 at 12:36
  • I'm having trouble seeing how the problem of choosing 3 random points in a triangle is the same as choosing 1 random point in the triangle, using the point (0,0) and a 3rd point that is determined by the first random point. – futurebird Feb 03 '20 at 12:39
  • 1/12 seems reasonable though... hm. – futurebird Feb 03 '20 at 12:40
  • I like the simplicity of the 3rd answer to the problem you linked. I'm going to think about a way to answer this problem in a similar way. – futurebird Feb 03 '20 at 12:42
  • You're over complicating things. I solved this question of yours about diagonal vertices soon after back when I answered the other post about adjacent vertices. Just setup an integral like the integral answer posted by Maxim. Or do you want to me type it up? – Lee David Chung Lin Feb 03 '20 at 12:44
  • nah I'm trying to work out what the 12 events would be so I won't need integration. – futurebird Feb 03 '20 at 12:57
  • To clarify, (1) by complicated things I mean the whole "...3 random points in a triangle..." (2) You won't find the 12-fold symmetry for this case. You will need to do the integral. – Lee David Chung Lin Feb 03 '20 at 12:58
  • 1
    At best you'll need to justify why each of the 4 identical events only contribute one-third-intersection, so to speak. That is, under the configuration that all 4 events drawn simultaneously, there's still no intersection in 2/3 of the region, and only 1/3 of the area gives you exactly one intersection. – Lee David Chung Lin Feb 03 '20 at 13:03
  • Very glad to know I was very wrong (maybe not totally) and that a better analysis exists. See the answer by Tony K. – Lee David Chung Lin Feb 03 '20 at 14:26

2 Answers2

4

We can do this without integrating anything. First, the two points must be on the same side of the diagonal; this introduces a factor of $\frac12$. Second, the two points, and the two corners, must form a convex quadrilateral (because the diagonals of a non-convex quadrilateral don't cross each other). Third, given such a convex quadrilateral, exactly one of the two assignments of points results in crossed lines, which introduces another factor of $\frac12$. So the final probability is $\frac14\times$ the probability that the four points form a convex quadrilateral.

Now, there is a linear transformation from the isosceles right-angled triangle to an equilateral triangle, that preserves areas (and therefore probabilities) and convexity. So this probability is the same as the probability that given two random points $X$ and $Y$ in an equilateral triangle $ABC$, the quadrilateral formed by $A,B,X,$ and $Y$ is convex. Here, by "the quadrilateral formed by..." I mean either $ABXY$ or $ABYX$, whichever is non-self-intersecting (but see comment below).

But given two such points $X$ and $Y$ in general position (by which I mean that no three of $A,B,C,X,Y$ are colinear), exactly one of the quadrilaterals formed by $A,B,X,Y$ or $B,C,X,Y$ or $C,A,X,Y$ is convex, depending on which of the three sides of the triangle is not crossed by the line through $XY$ (for instance, if the line through $XY$ doesn't cross side $BC$, then the quadrilateral formed by $B,C,X,Y$ is convex). So by symmetry, the probability that the quadrilateral formed by $A,B,X,Y$ is convex is $\frac13$.

Hence the final probability is $\frac{1}{12}$.

TonyK
  • 64,559
  • To nitpick my own answer: it may be that neither $ABXY$ nor $ABYX$ is non-self-intersecting. But not if one of them is convex, so I think my answer hangs together. Formally, it would be better to say something like "the points $A,B,X,Y$ admit a convex quadrilateral" or somesuch; but I don't think that would be easier to follow. – TonyK Feb 03 '20 at 14:39
2

$\renewcommand{\dd}[1]{\,\mathrm{d}#1}$Following your own diagram, due to symmetry it suffices to consider the region above the diagonal $h>g$ then multiply by two.

$$\text{Pr} = \text{area of shaded triangle} = 2 \int_{h=0}^1 \int_{g=0}^h \frac12 g \frac{h-g}{1-g}\dd{g}\dd{h} = \frac1{12}$$ where the integrand is the triangle with height $g$ and base width $\frac{h-g}{1-g}$. (There's a "typo" in the bottom two lines of the transcript: the denominator is $1-g$, not $1-h$)

In case one doesn't know how to do this integral, here's Wolfram Alpha code Integrate[g(h-g)/(1-g),{h,0,1},{g,0,h}].

Lee David Chung Lin
  • 7,043
  • I'm a little confused since g < h why are the limits of the inner integral from g=h to g=1 and not g=0 to g=h? The answer is the same, so I think it's just the area of the triangle reflected in y=x, the diagonal. – futurebird Feb 03 '20 at 14:07
  • Sorry that was a typo. I was using a different set of variables before switching to yours. – Lee David Chung Lin Feb 03 '20 at 14:08