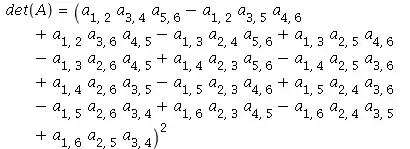Is it true that $\det(A-A^T) \geq 0$ for all $A \in \mathbb{R}^{n\times n}$?
For $n = 2$, this says that $\det\begin{pmatrix} 0 & a_{1,2}-a_{2,1} \\ a_{2,1}-a_{1,2} & 0 \end{pmatrix} \geq 0$, which is easily confirmed (the determinant is $\left(a_{1,2}-a_{2,1}\right)^2$ in this case).
$A-A^T$ is skew-symmetric so its complex eigenvalues are $0$ or purely imaginary. If $0$ is an eigenvalue, $\det(A-A^T)=0$ and the inequality holds.
Otherwise, since $A-A^T$ has real entries, complex eigenvalues come in conjugate pairs and $$\det(A-A^T) = \prod_i \lambda_i \overline{\lambda_i} = \prod_i |\lambda_i|^2 \geq 0$$
A proof that doesn't use complex eigenvalues:
Let $B = A - A^T$. We note that $B^T = -B$. Note that for any vector $x$, we have $x^TBx = 0$ since $$ x^TBx = (x^TBx)^T = x^TB^Tx = -(x^TBx). $$
Claim: For any $t > 0$, $\det(B + tI) \neq 0$.
Proof: Suppose for contradiction that $(B + tI)$ is singular. Let $x$ be a non-zero element of $\ker(B + tI)$. We have $$ (B + tI)x = 0 \implies Bx = -tx \implies x^TBx = x^T(-tx) \implies 0 = -t(x^Tx), $$ which is a contradiction. $\qquad \square$
Now, consider the polynomial $p(t) = \det(B + tI)$ over the domain $[0,\infty)$. We note that $p(t)$ has no zeros on the interval $(0,\infty)$, and (by the continuity of the determinant) $$ \lim_{t \to \infty} \frac{p(t)}{t^n} = \lim_{t \to \infty}t^{-n}\det(B + tI) = \lim_{t \to \infty} \det(t^{-1}B + I) = \det(0 \cdot B + I) = 1. $$ Thus, $\lim_{t \to \infty}p(t) = +\infty$. By the intermediate value theorem, we can conclude that $p(t)$ is positive over the interval $(0,\infty)$.
By the the continuity of $p$, we can conclude that $p(0) = \lim_{t \to 0^+} p(t) \geq 0$, which is to say that $\det(B) \geq 0$, which was the desired conclusion.
$A-A^T$ is skew-symmetric. It is well-known that all odd-sized skew-symmetric matrices are singular. So, it suffices to prove that every even-sized skew-symmetric matrix $K$ has a nonnegative determinant.
This can be proved by mathematical induction. The base case where the matrix is $2\times2$ is easy. In the induction step, consider an even-sized skew-symmetric matrix $K$. The result follows immediately if $K=0$. Suppose $K$ is nonzero. Then it must contain a nonzero principal $2\times2$ matrix $K_1$. Without loss of generality, we may assume that $$ K=\pmatrix{K_1&-B^T\\ B&K_2}. $$ Since $K_1$ is nonzero and skew-symmetric, it is nonsingular. It follows that the Schur complement $K_2-BK_1^{-1}B^T$ exists and is skew-symmetric. The result now follows from the identity $\det(K)=\det(K_1)\det(K_2-BK_1^{-1}B^T)$ and the induction hypothesis.
The result can be generalized as follows -and that is known since 1849 (Jacobi and Cayley)-.
$\textbf{Proposition}$. Let $A\in M_n(R)$ where $R$ is a commutative ring and $A$ is skew-symmetric.
Then $\det(A)$ is the square of an element of $R$.
For a proof, cf.
https://en.wikipedia.org/wiki/Pfaffian
https://core.ac.uk/download/pdf/82800447.pdf
For example, when $n=6$
