0

I am sorry for bothering you with this since there might be some very obvious answer but still: just stumble upon some old trigonometry stuff and realized that:

sin(0π) ≠ 0 & sin(π/2) ≠ 1 & sin(3π/2) ≠ -1

but answer to all those sinus inputs should be undefined since all those numbers(0, 1, -1) are actually limits, we can not have ratio of 0 since that would mean that there is an angle 0 which is not possible in the right triangle.

The same applies for 1 and -1 since there can not be 2 right angles in a triangle:).

then, subsequently:

the range of sinus

is not [-1, 1] but rather: (-1, 0) and (0, 1)

the domain (inputs) of sinus are:

all x in Real numbers |

x % π != 0 # <- otherwise get us ratio of 0 which is impossible

x % π/2 != 0 # <- otherwise get us ratio of 1 which is impossible

x % 2π/3 % != 0 # <- otherwise get us ratio of -1 which is impossible

the graph then should look like this, with the points excluded from the plot:

sinus(x)

My question is: why my thinking is wrong?

Otherwise all those fancy things like Euler's identity wont work for π for example

e^(iπ) = cos(π) + isin(π)

would mean that:

e^(iπ) = undefined + i * undefined

which does not make sense.

Are all those -1, 0, 1 values just a little helper crutches to keep us going so the math will "somehow" work?

  • the same applies for cosinus function of course ** sorry for some awkward notations, I am degenerated by programming
Jam
  • 10,325
myname
  • 1
  • 1
    Suppose we agreed (which I don't) that you cannot give values to $\sin0$ etc on the basis of geometry. What is to stop us nonetheless defining $\sin 0=0$, thus extending the function to include 0 in its domain? – almagest Jan 23 '20 at 18:31
  • We typically don't define the sine with reference to triangles in higher level mathematics. I would define the sine function by its series representation for example;$$\sin{(x)}=\sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{(2n+1)!}$$ – Peter Foreman Jan 23 '20 at 18:34
  • The ratio of sides in a right triangle cannot be negative either. Plus we cannot have angle greater than a right angle. You need a different definition of sine/cosine, for example, using unit circle or power series. – Vasili Jan 23 '20 at 18:48
  • 1
    Thank you @PeterForeman - seems reasonable – myname Jan 23 '20 at 18:52

3 Answers3

1

Extension of function domains

Functions are fundamentally relations between sets. In particular, they map values from a domain (e.g., the set $\{a,b,c\}$) to a range (e.g., $\{2,13,7\}$).

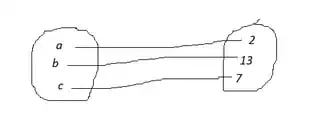
enter image description here

But for anything outside the domain, the function effectively has free reign. It is not necessarily 'undefined' due to an inconsistency of the type incurred by division by zero. It may literally just be not yet defined there. So it's perfectly acceptable to redefine the function with an extended domain and define the values the function would take there.

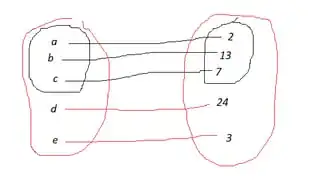
enter image description here

But then we can use this new, extended function wherever we would have used the old function. And since there's effectively no drawbacks, we may as well take a 'natural' extended function as the general definition. This is the case for exponentiation and factorials, which gives us widely agreed upon values for otherwise nonsensical expressions like $2^\pi$ and $(1/2)!$ and values of $\sin$. There is also the benefit of convenience. Why would we want two different functions for each domain and specify which one we mean each time we use them?

The geometric, right-angled-triangle definition of $\sin\theta=\frac{O}{A}$ is useful but has a limited domain and lacks some features that we would want (e.g., negative values). Indeed, one could argue that there is no triangle with a zero-length side, so this definition would not apply to $\sin0$. But other definitions (e.g., with the unit-circle, power series, differential equation) do allow for $0$ as an argument. So out of convenience, it is generally agreed that $\sin0=0$. If anything, your point should have gone further since no triangle can have an angle greater than $180^\circ$, so the triangle definition would only apply for $0<\theta<180^\circ$.

By the same logic, the power series definition of $\sin$ is a natural way of extending the domain to larger sets with entirely new elements. For example, the complex numbers. An angle of $(1+i)$ is meaningless but since we have a natural and consistent way of defining $\sin$ with its power series, we agree that $\sin\left((1+i)\ \mathrm{radians}\right)$ is well defined and equal to $1.298+0.635i$. And so on to even larger sets, like the quaternions (Question 1030737: Exponentiation of quaternions). We can carry on with these extensions ad infinitem, as long as we are consistent.

What is an angle of zero? - Degenerate cases

An angle between two line segments is often defined as the minimum rotation about a point needed to bring one into correspondence (i.e. on top of) the other (Mathworld), (Encyclopaedia Brittanica). But two coincident line segments that are already on top of each other and require no rotation. Therefore the angle between them should be zero. Likewise, if line segments are allowed to be zero-length, two coincident line segments form a degenerate triangle, in the same sense that a point is a degenerate circle. So then an angle of zero corresponds with a line segment of zero and $\sin0=0$ should arguably hold for the triangle definition too.

Community
  • 1
Jam
  • 10,325
  • thank you for examples, makes sense - I was locked up by the old definition(and realized through you example that by that same logic, we could also ban the 0 which does not makes sense). Anyway, used to exact definitions for each domain, which makes things more exact not complicated but in this case it really is the fault of the incomplete definition.. – myname Jan 24 '20 at 15:41
0

The domain of the sine function is all the real numbers. In real analysis, we do not define the trigonometric functions as ratios of the sides in a triangle.

For example, the sine function can be defined as

$$\sin(x)=\sum_{n=0}^{\infty}(-1)^n\frac{x^{2n+1}}{(2n+1)!}.$$

With some knowledge of infinite sums, it is possible to prove that the above sum is well-defined for all real $x$. No angles involved! And, it follows immediately from the definition that $\sin(0)=0$. We can define the cosine function in a similar way.

It can also be proved that, when restricted to the interval $(0, \pi/2)$ the function agrees with the usual definition using triangles.

Célio Augusto
  • 1,559
0

Although $\sin$ and $\cos$ can be used to describe the sides of right triangles that is not necessarily the definition of them.

If we use that as our definition then we can not define either for $x \le 0$ nor for $x \ge \frac \pi 2$.

But that doesn't have to be our definition.

Imagine a unit (radius $1$) circle centered at the origin $(0,0)$. We construct an central angle where the base ray is the $x$ axis starting and $(0,0)$ and point in the positive direction and the other ray is so that measure of the angle (measured in the clockwise direction from the $x$axis ray) is any measurement $\theta$. We needn't just have $0\le \theta \le \pi$ we can have $\theta < 0$ (the angle measures clockwise) or $\theta > \pi$ (the angle increases to a line and then continues to be "wider" than that line) and we can even have the angle be greater than $2\pi$ but having the angle go all the way around the circle and start all over again.

Okay. We have the circle and we have the angle $\theta$. Now look at the $(x,y)$ point on the circle that makes the angle.

We can define $\cos \theta = x$ and $\sin \theta = y$.

If we notice for $0 < \theta < \frac \pi 2$ that $(x,y)$ and $(x,0)$ and $(0,0)$ make a right triangle with hypotenuse $1$ and adjecent side $x$ and opposite side $y$ so this fits our "right triangle" definition.

If $\frac \pi 2 < \theta < \pi$ then $(x,y)$ and $(x,0)$ and $(0,0)$ still make a right triangle. But it's base goes in the "negative" direction. The angle is $\pi - \theta$ and the opposite side is still $y$ but the adjacent side is $|x| = -x$.

This is still okay but it extends your old definition.

fleablood
  • 124,253