$\lim_{n\to\infty}\sum_{k=1}^n\frac{1}{\sqrt[3]{kn^2}}$

Question

In the very beginning, I'm going to refer to an already posted question quite similar to mine:

Limit $\lim_{n\to\infty} n^{-3/2}(1+\sqrt{2}+\ldots+\sqrt{n})=\lim_{n \to \infty} \frac{\sqrt{1} + \sqrt{2} + ... + \sqrt{n}}{n\sqrt{n}}$

And, to give an insight into what I've examined already:

Limit of sum with cube roots.

Compute: $$\lim_{n\to\infty}\frac{1+\frac1{\sqrt[3]{2}}+\ldots+\frac1{\sqrt[3]{n}}}{\sqrt[3]{n^2}}$$

My attempt:

As in the references, I also thought of applying Stolz-Cesaro, and got the following:

$L=\lim\limits_{n\to\infty}\frac{1+\frac1{\sqrt[3]{2}}+\ldots+\frac1{\sqrt[3]{n}}}{\sqrt[3]{n^2}}=\lim\limits_{n\to\infty}\frac{\sum\limits_{k=1}^{n+1}\frac1{\sqrt[3]{k}}-\sum\limits_{k=1}^n\frac1{\sqrt[3]{k}}}{\sqrt[3]{(n+1)^2}-\sqrt[3]{n^2}}=\lim\limits_{n\to\infty}\frac{\frac1{\sqrt[3]{n+1}}}{\sqrt[3]{(n+1)^2}-\sqrt[3]{n^2}}$

To avoid L'Hospital, I've done this: $\begin{aligned}L&=\lim_{n\to\infty}\frac1{\sqrt[3]{n+1}\left(\sqrt[3]{(n+1)^2}-\sqrt[3]{n^2}\right)}\\&=\lim_{n\to\infty}\frac{1}{n+1-\sqrt[3]{n^2(n+1)}}\\&=\frac1{\infty-\infty}\\&=\frac1{\infty}=0\end{aligned}$

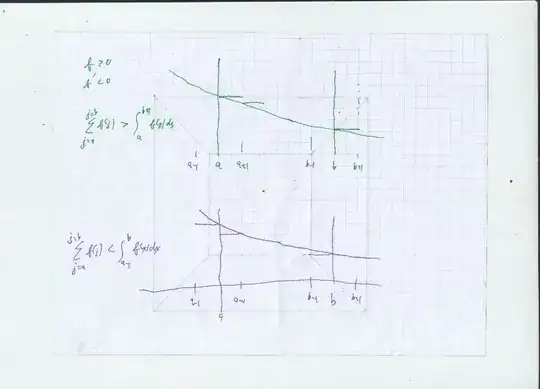
I was wondering if there were another elegant method apart from Riemann sum or already used Stolz-Cesaro that I could use because this task appeared in Analysis 1 exam. Stolz-Cesaro is allowed and there was no constraint on any other methods, but I'm not familiar to Riemann sums at all.

To ask explicitly(for the sake of developing new ideas):

For example: If I changed the order of the summands this way: $$\frac{1}{\sqrt[3]{n}}+\frac{1}{\sqrt[3]{n-1}}+\ldots+\frac{1}{\sqrt[3]{2}}+1$$ would that be of any use in an algebraic manipulation that would lead me on the right track? Final question: Is my answer:$L=0$ correct?

Answer 1

The limit of the ratio in your title is nonzero. Give me a few minutes to type up the following, based on your funtion $g(x) = x^{-1/3}$

if we have $g(x) > 0$ but $g'(x) < 0,$ then $$ \int_a^{b+1} \; g(x) \; dx \; < \; \sum_{j=a}^b \; g(j) \; < \; \int_{a-1}^b \; g(x) \; dx $$

Here is a drawing I made, using the letter $f$ rather than $g$

Well, $g$ is integrable at the origin. Let's try $a=1.$ If that is not satisfactory we can just switch to $a=2$ by putting in some extra terms.

$$ \int_1^{n+1} \; x^{-1/3} \; dx \; < \; \sum_{j=a}^b \; j^{-1/3} \; < \; \int_{0}^n \; x^{-1/3} \; dx $$

an antiderivative of $g$ is $G(x) = \frac{3}{2} x^{2/3}$

$$ \frac{3}{2} \left( (n+1)^{2/3} - 1 \right) \; < \; \sum_{j=1}^n \; j^{-1/3} \; < \; \frac{3}{2} n^{2/3} $$

Good enough. Your denominator is simply $ n^{2/3}.$ We see that $$ L = \frac{3}{2} $$

Answer 2

I think what you need is to rationalize the denominator. In fact \begin{eqnarray} &&\lim_{n\to\infty}\frac{\frac{1}{\sqrt[3]{n+1}}}{\sqrt[3]{(n+1)^2}-\sqrt[3]{n^2}}\\ &=&\lim_{n\to\infty}\frac{\sqrt[3]{(n+1)^4}+\sqrt[3]{(n+1)^2}\sqrt[3]{n^2}+\sqrt[3]{n^4}}{\sqrt[3]{n+1}((n+1)^2-n^2)}\\ &=&\lim_{n\to\infty}\frac{\sqrt[3]{(n+1)^4}+\sqrt[3]{(n+1)^2}\sqrt[3]{n^2}+\sqrt[3]{n^4}}{2n\sqrt[3]{n+1}}\\ &=&\frac32. \end{eqnarray}

Answer 3

How about a Riemann sum? $$ \sum_{k=1}^n\frac{1}{\sqrt[3]{kn^2}} = \frac{1}{n}\sum_{k=1}^n\left(\frac{k}{n}\right)^{-1/3} \to \int_0^1 x^{-1/3}\;dx = \frac{3}{2} $$ I guess this calculation is merely "suggestive", since the integral is improper. (See my answer at https://math.stackexchange.com/a/482107/442 for an example where Riemann sum fails on a convergent improper integral.)

To make this argument rigorous, do this: Let $f(x) = x^{-1/3}$ on $(0,1)$. Then $f \ge 0$ and $\int_0^1 f = 3/2$. Now for a fixed $n$, let $$ g_n(x) = \left(\frac{k}{n}\right)^{-1/3}\quad \text{for } \frac{k-1}{n}<x \le\frac{k}{n},\quad k=1,2,\dots,n . $$ Then $0 < g_n \le f$ and $g_n \to f$ pointwise, so by the dominated convergence theorem, we get $\int_0^1 g_n \to \int_0^1 f$.