Calculating the normal vector to a space curve to construct a 3D plot

Question

In trying to follow the calculation of the normal curvature of a curve $C$ at a point $P,$ using Geogebra and a somewhat random example, I got stuck. Here is what I did:

The surface $S$ was set up as with domain boundaries for $-1<x<1$ and $-1<y<1$ as:

$$f(x,y)=-x^2+\cos(x)+\cos(y)$$

The space curve $C\in \mathbb R^3$ was parametrized by $t$ with $-1<t<1$ as:

$$C(t)=(t,t^2,f(x,y))$$

With $x=t$ and $y=t^2.$

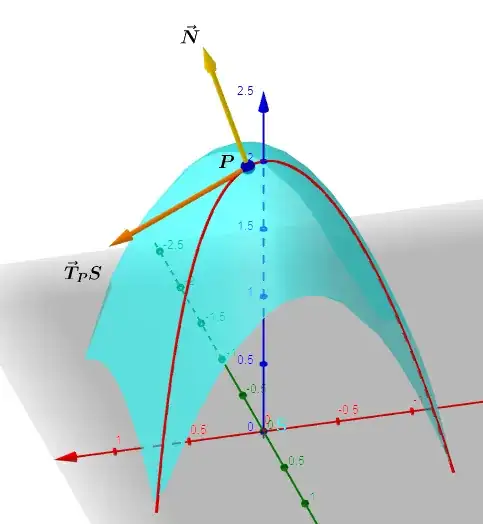
The normal vector to the surface $\vec N$ was calculated as:

$$\vec N(t)=\left (-\frac{\partial f}{\partial x}\frac{\partial x}{\partial t} ,-\frac{\partial f}{\partial y}\frac{\partial y}{\partial t},1\right)=\left(2t+\sin(t),\sin(t^2),1\right)$$

The tangent vector at point $P$ ($\vec T\in T_PS)$ was calculated as

$$\vec T(t) =\frac{d}{d t}C(t) =\left(1,2t,-2t-\sin(t)-2t\sin(t^2)\right)$$

This seemed to result in a plausible plot:

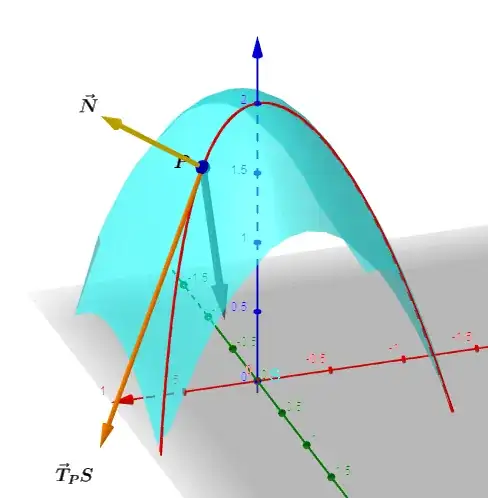
However, the calculation of the normal vector to $C$ at $P$ was not so happy:

$$\vec n=\frac{\vec T'}{\vert T\vert}=\frac{(0,2,-2\sin(t^2)-4t^2\cos(t^2)-2-\cos(t))}{\vert T\vert}$$

which would yield something like this (black arrow):

clearly not orthogonal to $\vec T.$

Where did I go wrong in this calculation of the normal vector of $C$ at $P$?

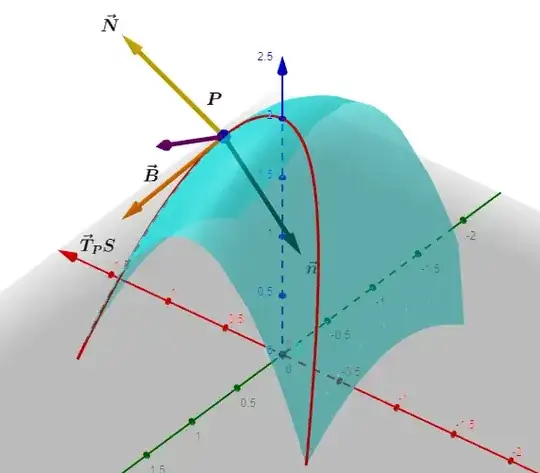
I would like to calculate this normal vector to the curve by differentiation; however, the only way I have been able to produce some plausible plot is by first calculating the binormal vector:

$$\vec B=\frac{T\wedge T'}{|T\wedge T'|}$$

to later do the cross product of $\vec T$ with $\vec B:$

Answer 1

Great question, with really nice pictures and explanations of what you've done so far.

First step: Heed @David's advice about $t$ and $t^2$. :)

But there is still another problem:

The normal is defined to be the derivative of the UNIT tangent. The thing you've called "$T$" isn't the unit tangent vector, and should really be given some temporary name, say, $U$, and then you define $$ T(t) = \frac{1}{\|U(t)\|} U(t) $$ which is always a unit vector, i.e., you have $$ T(t) \cdot T(t) = 1 $$ Take the derivative with the product rule, and you get

$$ T'(t) \cdot T(t) + T(t) \cdot T'(t) = 0 $$ so that $$ T'(t) \cdot T(t) = 0 $$ as expected. But if you compute $U'(t)$, it's likely, in all but exceptional cases, to have a large component in the $T(t)$ direction.

Post-comment addition Replacing $T$ with $U$ as I suggested gives $$\vec U(t) =\frac{d}{d t}C(t) =\left(1,2t,-2t-\sin(t)-2t\sin(t^2)\right)$$ so that \begin{align} \| U(t) \|^2 &= 1^2 + 4t^2 + (2t + \sin t + 2t \sin(t^2))\\ &= 1 + 4t^2 + 4t^2 + \sin^2t + 4t^2 \sin^2 t^2 \\ & + 4t \sin t + 4t^2 \sin(t^2) + 4t \sin t \sin t^2\\ &= 1 + 8t^2 + (1 + 4t^2) \sin^2 t + 4t^2 \sin^2 t^2 + 4t \sin t + 4t \sin t \sin t^2\\ \end{align} which is definitely not a constant, and the square root of that mess isn't a constant either. So $U'(t)$ and $T'(t)$ are not even close to being proportional.

There is something useful you can do with $U'$ however: you can apply Gram-Schmidt to $U$ and $U'$ to get the component of $U'$ that's perpendicular to $U$. Here goes:

COmpute

$$ S(t) = U'(t) - \frac{(U'(t) \cdot U(t)}{(U(t) \cdot U(t)} U(t) $$ This evidently lies in the plane spanned by $U$ and $U'$, and (take its dot-prod with $U(t)$ to see this) it is *perpendicular to $U(t)$. Hence it's some multiple of the thing you were looking for, the unit normal $N(t)$.

So to find $N(t)$, you just compute

$$ N(t) = \frac{1}{\|S(t)\|} S(t). $$

And there you have it -- no need to normalize $U$ in advance with a hideous square root.