Why is the normal vector in Frenet-Serret triad moving in inverse direction to the norm of the curvature?

Question

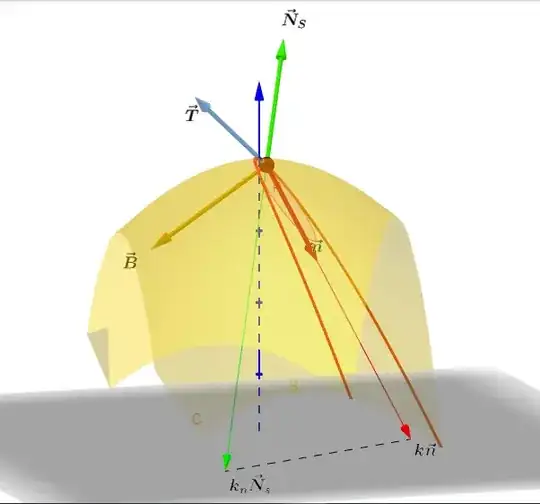
I have been working on a representation of the Frenet-Serret vectors at a point of a curve on a surface embedded in $\mathbb R^3,$ utilizing built-in equations in Geogebra, and trying to reproduce the results with "manual" expressions following the cross product formulas in here.

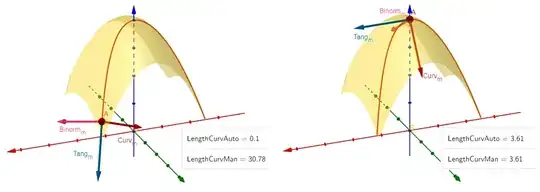
The problem is that, although the normal vector $\text{Curv}_m$ is in the right direction, its norm seems to move in opposite direction using the built-in formula as compared to the manually typed cross product $\left(T(t)\times T'(t)\right)\times T(t).$ This is very apparent upon visual inspection: for instance, comparing the values at the point of least curvature to the point with maximum curvature, where the values converge:

Before normalizing these vectors (as they appear on the graphs), the length of the normal vector at a point along the relatively straight segment is close to $0$ using the built-in formulas, whereas it is $30$ using the cross-product formula. At the top, markedly curved part, the values are similar at around $4$ with both methods.

Why is the cross product moving in inverse norm value as the actual curvature? And is there any adjustment that would correct this?

Requested in comments:

Underlying surface/curve:

The surface $S$ was set up as with domain boundaries for $-1<x<1$ and $-1<y<1$ as:

$$f(x,y)=-x^2+\cos(x)+\cos(y)$$

The space curve $C\in \mathbb R^3$ was parametrized by $t$ with $-1<t<1$ as:

$$C(t)=(t,t^2,f(x,y))$$

With $x=t$ and $y=t^2.$

Could you be more specific on what curve and what surface you consider? — WimC, Jan 18 '20 at 18:43
I don't understand what you mean by its "norm." This must be a language issue. The Frenet frame has nothing to do with the surface. You're talking about the geodesic curvature of the curve in the surface, and it has a sign — it can be positive or negative, depending on the relation of the Frenet normal $N$ with the vector you specified. — Ted Shifrin, Jan 18 '20 at 18:48
It may help for others to get some context by reading an earlier question that led to this one: https://math.stackexchange.com/questions/3510852/calculating-the-normal-vector-to-a-space-curve-to-construct-a-3d-plot/3511972?noredirect=1#comment7226599_3511972 — John Hughes, Jan 18 '20 at 18:58
Note, the "wedge product" often refers to the exterior product, which is associative, and works in any number of dimensions. I recommend "$\times$" for the 3D vector cross product. — mr_e_man, Jan 19 '20 at 21:52
@mr_e_man Out of curiosity, check these few seconds in this talk vis-a-vis cross-product versus wedge in this context. — Antoni Parellada, Jan 20 '20 at 00:14

score 1 · Answer 1 · answered Jan 19 '20 at 20:21

The normal curvature of the curve $C$ at the point $A$ can be found as

$$\vec n(s)=\frac{T'(s)}{\vert T'(s)\vert}=\frac 1k T'(s)$$

provided the curve is arc-length parameterized, and since $\vert T'(s)\vert$ is the curvature of the curve at $s.$

However this seems to have practical challenges in differentiating functions with cumbersome square roots in the normalizing denominators.

The "trick" in the code used to generate $\left(T(t)\wedge T'(t)\right)\wedge T(t)$ the vector is simply meant to obtain a vector in the direction of $\vec n.$ However, it will have to be normalized to unit, in which case it will only represent the curvature if its multiplied by $k,$ resulting in $k\vec n.$ In turn, $k$ can be calculated as

$$k(t)=\frac{C'(t)\wedge C''(t)}{\vert C'(t)\vert^3}$$

The projection of $k\vec n$ on the line spanned by the normal vector to the surface at $A$ results in $k_n=k\cos\theta:$

Why is the normal vector in Frenet-Serret triad moving in inverse direction to the norm of the curvature?

1 Answers1