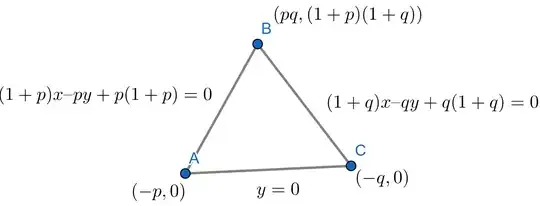
Find the locus of the orthocenter of the triangle formed by the lines $(1 + p)x – py + p(1 + p) = 0$, $(1 + q)x – qy + q(1 + q) = 0, y = 0$ where $p\ne q$
My attempt is as follows:-
Equation of perpendicular from $B$ to $AC$ will be $x=pq$
As orthocenter will lie on it, so $h=pq\tag{1}$
Equation of perpendicular from $C$ to $AB$ will be $(1+p)y+px+pq=0$
As orthocenter will lie on it, so $(1+p)k+ph+pq=0\tag{2}$
Equation of perpendicular from $A$ to $BC$ will be $(1+q)y+qx+pq=0$
As orthocenter will lie on it, so $(1+q)k+qh+pq=0\tag{3}$
Subtracting equation $(3)$ from $(2)$
$$(p-q)k+(p-q)h=0$$
As $p\ne q$,so $k+h=0$
So locus of orthocenter is $h+k=0$
But is this correct? Actual answer is just "straight line", so that's why I am not sure whether this is the correct locus or not.