Three properties of a parabola with three tangents

Question

About ten days ago I discovered three beautiful properties of a parabola with three tangents drawn using the GeoGebra program. I would like to get proof of these properties and also know if any of them have been discovered before or not.

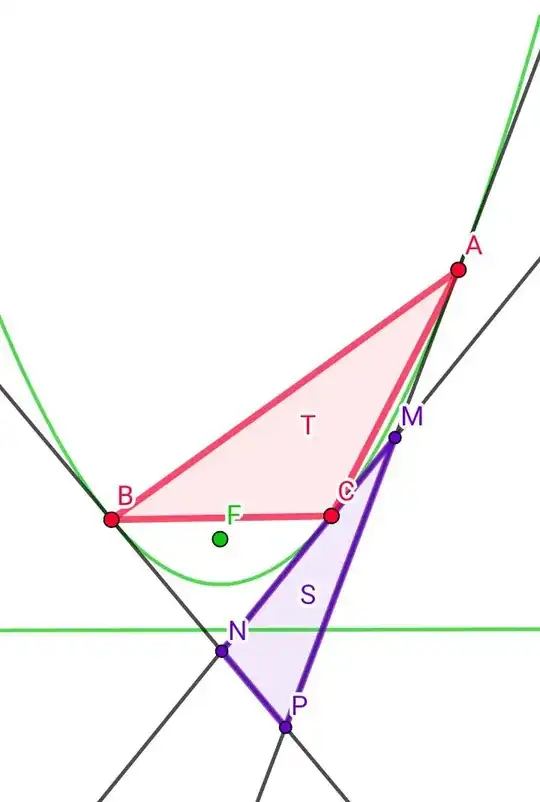
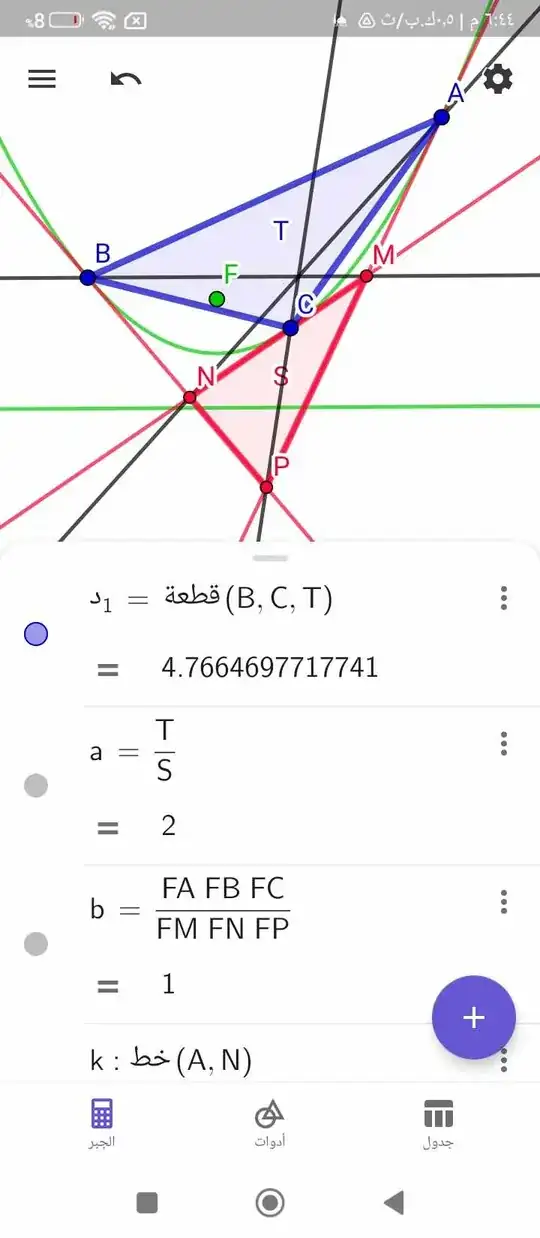
We have a parabola, and we chose three points from it, $A$, $B$, and $C$. We drew the tangents to the parabola in them, which enclose the triangle $∆MNP$, so the area of triangle ABC will be equal to twice the area of triangle $∆MNP$. In other words $T=2S$

Another beautiful property is achieved in the form: $\frac{FA×FB×FC}{FM×FN×FP}=1$

Also, the lines $AN$, $BM$, and $CP$ converge at one point

The first property is known : see here. I didn't know the second property nor the third. — Jean Marie, Nov 22 '23 at 20:09
A little remark : you don't need figure 1. Figure 2 is enough. — Jean Marie, Nov 22 '23 at 22:12
A result that could be helpful : Lambert's theorem asserting that the circumcircle of triangle MNP passes through focus $F$. — Jean Marie, Nov 22 '23 at 22:43
Another useful result : the fact that the orthocenter of triangle $MNP$ belongs to the directrix of the parabola can be found in this answer of mine here. — Jean Marie, Nov 23 '23 at 01:55
Thank you very much, yes I know Lambert's theorem, but I did not know that the first property was previously discovered, but it is expected because it is an elementary property of the parabola — زكريا حسناوي, Nov 23 '23 at 02:03
I wonder if the opposite is true. What if we were looking for the locus that satisfies the property that the area of its triangle is equal to twice the area of the tangent triangle? Would we get a parabola or would the locus be larger than that? — زكريا حسناوي, Nov 23 '23 at 02:05
The third property appears to be general to all conic sections — زكريا حسناوي, Nov 23 '23 at 02:12

score 1 · Answer 1 · answered Nov 24 '23 at 21:09

Let's prove the third property in the special case of a circle: as projective transformations preserve collinearity, the result holds for any conic section.

The proof follows from the converse of Ceva's theorem applied to triangle $PMN$: lines $PC$, $AN$, $BM$ concur if:

$$ {BN\over BP}\cdot{AP\over AM}\cdot{CM\over CN}=1. $$ But that is trivially true, because $$ BN=CN,\quad BP=AP,\quad AM=CM. $$

Three properties of a parabola with three tangents

1 Answers1