Calculate web distance‽?

Question

I am doing the following programming exercise: The Spider and the Fly (Jumping Spider). The statement is:

Background

A spider web is defined by

"rings" numbered out from the centre as 0, 1, 2, 3, 4

"radials" labelled clock-wise from the top as A, B, C, D, E, F, G, H

Here is a picture to help explain: Web Coordinates

As you can see, each point where the rings and the radials intersect can be described by a "web coordinate".

So in this example the spider is at H3 and the fly is at E2 Kata Task

Our friendly jumping spider is resting and minding his own spidery business at web-coordinate spider.

An inattentive fly bumbles into the web at web-coordinate fly and gets itself stuck.

Your task is to calculate and return the distance the spider must jump to get to the fly. Example

The solution to the scenario described by the picture is 4.63522 Notes

The centre of the web will always be referred to as A0
The rings intersect the radials at evenly spaced distances of 1 unit

I was trying to do by hand the calculus to solve the example:

Fist intuition was to give to each radial, a value: A 0, B 1, C 2, D 3, E 4, F 5, G 6, H 7

Considering the example where we are at: x1,y1: H3 x2,y2: E2; it could be thought as x1,y1: 7,3 x2,y2: 4,2

Then my first way to try to solve the distance was to use: x2-x1 + y2-y1; 4-7 + 3-2 = 3+1 = 4

My second attempt to calculate the distance was with the distance between two points: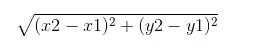

$\displaystyle \sqrt{( 4-7)^{2} +( 2-3)^{2}}$ $\displaystyle =\ \sqrt{3^{2} +1^{2} \ } \ =\ \sqrt{10} \ =3,162277660168379‬\ $

As you see, none of the previous ideas achieve to calculate the example as it is been given in the exercise.

In addition I have also read:

• A natural-looking distance formula
• To understand the distance function in (X, || . || ) × ( X, ||. || )
• Calculate distance between two points N,W,E,S

How could we calculate the web distance‽?

Answer 1

You could consider the complex plane and complex numbers. Assuming A is $0$, B is $1$, ...H is $7$, ..., the spider is on coordinates $(7,3)$ and the fly in on $(4,2)$. In the complex plane those places are $3 \left( \cos {\frac{3\pi}{4}}+i\sin {\frac{3\pi}{4}}\right)$ and $2 \left( \cos {\frac{3\pi}{2}}+i\sin {\frac{3\pi}{2}}\right)$. So, in the algebraic form, we have $-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i$ for the location of the spider and $-2i$ for the location of the fly. Now you can calculate the absolute value of the difference between those values to get the distance:

$$d=\left|\left(-\frac{3\sqrt{2}}{2}+\frac{3\sqrt{2}}{2}i\right)-\left(-2i\right)\right| =\sqrt{\left( \frac{3\sqrt{2}}{2} \right)^2+\left(2+ \frac{3\sqrt{2}}{2} \right)^2 } \approx 4.63522$$

For a general formula, you just have to repeat the process keeping in mind that a set of coordinates $(a,b)$ in the web system corresponds to the complex number $b \left( \cos {\frac{(2-a)\pi}{4}}+i\sin {\frac{(2-a)\pi}{4}}\right)$.

Answer 2

\begin{eqnarray*} d= \sqrt{\left( 2+ \frac{3}{\sqrt{2}} \right)^2 + \left( \frac{3}{\sqrt{2}} \right)^2 } = 4.6522 \cdots. \end{eqnarray*}