Instead of talking about distances $D(x,y)$ it is slightly easier to talk about norms $$N(x-y).$$
Your proposes $D_3$ is called the $L_3$ norm and is part of a family of norms
$$\|x\|_p = \left(|x_1|^p + \ldots + |x_n|^p\right)^{1/p}$$
called the $L_p$ norms. For $p\geq1$ they obey all of the properties needed for a norm: positive for nonzero $x$, linear under multiplication by positive scalars, and satisfy the triangle inequality.
$p=2$ is the usual Euclidean norm and induces the usual Euclidean distance. In one dimension, all of the $L_p$ norms are equivalent, which is why you interpreted the $L_2$ norm as the $L_1$ norm.
So to answer your question, nothing goes wrong when you use the $L_3$ norm. You will get lengths that are somewhere between using the usual $L_2$ norm, and the $L_{\infty}$ or "max" norm which returns the magnitude of the largest component; as such, components of a vector that are small relative to the largest components will tend to get ignored by an $L_3$ ruler.
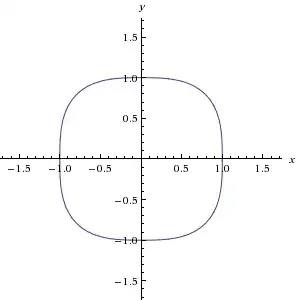
Here's what the unit circle would look like using such a norm: