Po-Shen Loh's new way of solving quadratic equation

Question

Quadratic equation, $ax^2+bx+c=0$ and its solution is quadratic equation, $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Now setting $a=1$ then we have $x^2+bx+c=0$

$$x=\frac{-b\pm \sqrt{b^2-4c}}{2}$$ rewrite as

$$x=-\frac{b}{2}\pm \sqrt{\left(\frac{b}{2}\right)^2-c}$$

In this new video Dr. Loh claims to discover a new way of solving the quadratic equation! How? It is the same as the above formula, by using the quadratic formula, the only thing I see different, is he rewrite it in the above form!

Can someone please explain to me how this is a new way?

Answer 1

For $b^2-4ac\geq0$ and $a=1$ they are the same: $$\frac{-b+\sqrt{b^2-4ac}}{2a}=\frac{-\frac{b}{2}+\sqrt{\frac{b^2-4ac}{4}}}{a}=\frac{-\frac{b}{2}+\sqrt{\left(\frac{b}{2}\right)^2-ac}}{a}=-\frac{b}{2}+\sqrt{\left(\frac{b}{2}\right)^2-c}$$ and $$\frac{-b-\sqrt{b^2-4ac}}{2a}=\frac{-\frac{b}{2}-\sqrt{\frac{b^2-4ac}{4}}}{a}=\frac{-\frac{b}{2}-\sqrt{\left(\frac{b}{2}\right)^2-ac}}{a}=-\frac{b}{2}-\sqrt{\left(\frac{b}{2}\right)^2-c}.$$

Answer 2

Let us illustrate by example. Consider the equation \begin{align} x^2-2019x-2020 = (x-r_1)(x-r_2) = x^2-(r_1+r_2)x+r_1r_2=0. \end{align} The key observation is that the roots $r_1, r_2$ adds up to $2019$, which means the average of $r_1$ and $r_2$ is $\frac{2019}{2}$. Hence the roots have the form $r_\pm = \frac{2019}{2}\pm z$ for some $z$.

Next, it follows \begin{align} \frac{(2019)^2}{4}-z^2 = r_1r_2 = -2020 \ \ \implies \ \ z = \sqrt{\frac{(2019)^2}{4}+2020}. \end{align} Thus, we have \begin{align} r = \frac{2019}{2}\pm \sqrt{\frac{(2019)^2}{4}+2020}. \end{align} The "new" aspect is that the derivation avoids completing the square.

Here's another example \begin{align} x^2+212323x+24434 = 0 \end{align} Again, the roots should have the form \begin{align} r_\pm = -\frac{212323}{2}\pm z \ \ \implies \ \ \frac{(212323)^2}{4}- z^2= 24434 \end{align} which means \begin{align} z = \sqrt{\frac{(212323)^2}{4}-24434} \ \ \implies \ \ r_\pm = -\frac{212323}{2}\pm \sqrt{\frac{(212323)^2}{4}-24434}. \end{align}

Answer 3

Here's a geometric justification of the approach.

---

Suppose $P:=(p,0)$ and $Q:=(q,0)$ are points on the positive $x$-axis. (See Note for when $p$ and $q$ differ in sign.) Consider a (semi-)circle with diameter $\overline{PQ}$.

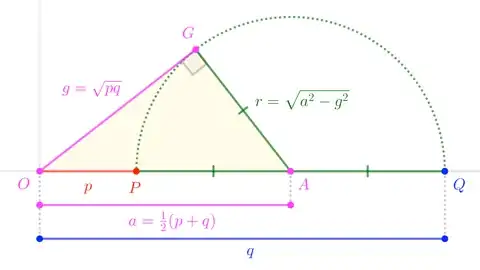
If $A$ is the center of that circle, then $$a := |OA| = \frac12\left(|OP|+|OQ|\right) = \frac12(p+q) \tag1$$ If $G$ is the point where the tangent from $O$ meets the circle, then (by the Power of a Point theorems), $$|OG|^2 = |OP||OQ| \quad\to\quad g := |OG| = \sqrt{pq} \tag2$$ (Thus, $a$ is the arithmetic mean of $p$ and $q$, while $g$ is the geometric mean, which may explain my choice of variable names.) If $r$ is the radius of the circle, then we clearly have that $P$ and $Q$ are at distance $r$ from $A$, so that (abusing notation slightly) $$\{p,q\} \;=\; a \pm r \tag3$$ But $\triangle OAG$ has a right angle at $G$, so that Pythagoras tells us $a^2 = g^2 + r^2$. Solving for $r$, we can write

$$\{p,q\} \;=\; a \pm \sqrt{a^2-g^2} \tag{$\star$}$$

That is, $(\star)$ tells us how to calculate two numbers ($p$ and $q$) from their means ($a$ and $g$). Nifty.

Now, the relevance to the Quadratic Formula comes from supposing that the monic quadratic polynomial $x^2+Bx+C$ has those numbers $p$ and $q$ as roots. We "know" that this means the polynomial must factor as $$x^2 + Bx + C = (x-p)(x-q) = x^2-(p+q)x + pq \tag4$$ Comparing coefficients, we have $$B = -(p+q) \qquad\qquad C = pq \tag5$$ This shows that $B$ is the negative of the sum of the roots, and $C$ is the product. (Vieta's formulas generalize this observation to general polynomials.) In the context of our geometric argument, $B$ is the negative of twice the arithmetic mean, and $C$ is the square of the geometric mean. $$B = -2a \qquad\qquad C = g^2 \tag6$$ Substituting $a=-B/2$ and $g^2=C$ into $(\star)$ gives Loh's preferred form of the (monic) Quadratic Formula:

$$\{p,q\}\;=\;-\frac{B}2\pm\sqrt{\left(\frac{B}2\right)^2-C} \tag{$\star\star$}$$

I may myself prefer to think of this as "$(\star)$ + Vieta".

---

Note: Adjusting the argument for $P$ and $Q$ on opposite sides of $O$ (corresponding to quadratic roots differing in sign) gets a little fiddly depending upon how we introduce negatives into the geometry. Here, we'll consider $p$, $q$, and $a$ to be signed distances; this allows us to maintain the relation $a=\tfrac12(p+q)$. The figure for this case takes $G$ to be the point where the perpendicular at $O$ meets the circle; its (unsigned) length is the geometric mean of unsigned lengths $|OP|$ and $|OQ|$, so we write $g = \sqrt{|pq|}$.

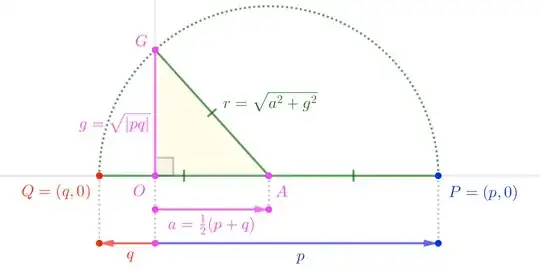
Again, $\triangle OAG$ is a right triangle, but $r$ is now the hypotenuse, giving the counterpart of $(\star)$ this form:

$$\{p,q\} \;=\; a \pm\sqrt{a^2+g^2} \tag{$\star'$}$$

Taking $p$ and $q$ to be roots of $x^2+Bx+C$ as before, we still have relations $(5)$, because the signs of the roots don't affect the algebra leading to those relations. However, the signs do require us to write $g^2= -C$ (because $g^2=|pq|^2$ is positive, while $C=pq$ is negative). But this weirdness exactly cancels the Pythagorean sign change in $(\star')$, so that substitution gives us $(\star\star)$ again. Convenient, that.

Final tweaks to show that $(\star\star)$ also holds for $p$ and $q$ both negative, or when one or both vanish, are left as exercises to the reader.

Answer 4

Well, notice that the $2$ in the denominator has been absorbed into the radical. Thus instead of $\sqrt{b^2-4c}$, we have $\sqrt{(b/2)^2-c}$.

Answer 5

Nothing about the standard quadratic formula is really intuitive. Sure, you can derive it by completing the square, but that gets complicated, and isn't really an accessible proof on the level of those learning to solve quadratics for the first time. However, Loh's method builds on an understanding of both factoring and graphing.

For example, $x^2 – 10x + 21$ factors as $(x-3)(x-7)$ and therefore has the solutions $3$ and $7$. Notice that $B=-10=-(3+7)$ and $C=21=(3)(7)$. Therefore $-B$ is the sum of the solutions, and $C$ is the product of the solutions. Both of these facts will be needed.

Now consider the graph of $y=x^2 – 10x + 21$ shown below. To use Loh's method, we'll need two other variables: $m$ and $d$. Where $(m, 0)$ is the midpoint of the zeros, $m$ is the average of the solutions. Then $d$ is the distance each zero is from the midpoint. Therefore, we can represent the solutions as $m-d$ and $m+d$ or as just $m \pm d$. If we could calculate $m$ and $d$ simply from $B$ and $C$, we'd have an easy way to solve a quadratic. And we can!

Let's get to Loh's method. We'll begin by assuming we have a quadratic of the form $Ax^2+Bx+C=0$ where $A=1$. We've already established that $-B$ is the sum of our solutions. Since the mean of the solutions is their sum divided by 2, $m=\frac{-B}{2}$. Also recall that $C$ is the product of the solutions. Therefore, $C=(m-d)(m+d)=m^2-d^2$. If we rearrange this as $d^2=m^2-C$, we have an easy way to find $d$ from $m$ and $C$. We can then write our solutions as $m \pm d$.

Here's how it works out with $y=x^2 – 10x + 21$.

$m=\frac{-B}{2}=\frac{10}{2}=5$

$d^2=m^2-C=(5)^2-21=4$

Therefore, $d=\pm \sqrt 4=\pm 2$

Since $m\pm d=5\pm 2$, the solutions are 3 and 7.

That's Loh's method! Again, it's far more accessible to students just learning how to solve quadratics.

I will admit, no one talks much about the case where $A\neq 1$. Sure, you can divide through by $A$ and not affect the roots, but it means fractions, accompanying fraction arithmetic, and the possible need to rationalize denominators--all of which is not necessary if just using the commonly memorized quadratic formula. Consider just trying to solve $3x^2 + 3x + 1 = 0$ and you'll see what I mean. You end up with fractions all the way through with denominators of 2, 3, 4, 6, and 12 at some point in the process. Plus, the connection made from here to the actual quadratic formula isn't nearly as intuitive and accessible as the rest of Loh's method. Before I posted this answer, I posted a related question and answer here that I think is better for when $A\neq 1$.

Answer 6

The teacher's conclusion at the end "guesswork has been replaced by a clever trick" implies that the main result of the proposed new method is the clever trick (change of unknowns $x_1$ and $x_2$) of solving the system of equations (which is the Vieta's theorem): $$\begin{cases}x_1+x_2=-b\\ x_1x_2=c\end{cases} \stackrel{x_1=\frac{-b}{2}-t\\x_2=\frac{-b}{2}+t}\Rightarrow x_1x_2=\frac{b^2}{4}-t^2=c \Rightarrow t=\pm \sqrt{\frac{b^2}{4}-c} \Rightarrow \\ x_1=\frac{-b}{2}-\sqrt{\frac{b^2}{4}-c}=\frac{-b-\sqrt{b^2-4c}}{2}\\ x_2=\frac{-b}{2}+\sqrt{\frac{b^2}{4}-c}=\frac{-b+\sqrt{b^2-4c}}{2}$$

Answer 7

Suppose that $A$ is the arithmetic mean of the roots of the quadratic $P$, and $R$ is the geometric mean [where $P(x) = ax^2+bx+c = a(x-r_1)(x-r_2)$], then we have this equation:

$$\begin{align} P(x) &= 0\\ ax^2+bx+c &= 0\\ x^2+\frac{b}{a}x+\frac{c}{a} &= 0\\ x^2+\beta x+\gamma &= 0\\ \end{align}$$ But we can also look at it from another point of view. $$\begin{align} a(x-r_1)(x-r_2) &= 0\\ (x-r_1)(x-r_2) &= 0\\ x^2 -(r_1+r_2)x+r_1r_2 &= 0\\ x^2 -2\bigg(\frac{r_1+r_2}{2}\bigg)x+\sqrt{r_1r_2}^2 &= 0\\ x^2 -2Ax+R^2 &= 0\\ \end{align}$$

which can be solved via completing the square. $$\begin{align} x^2-2Ax+R^2 &= 0\\ (x^2-2Ax+A^2)+(R^2-A^2) &= 0\\ (x-A)^2+(R^2-A^2) &= 0\\ (x-A)^2-(A+R)(A-R) &= 0\\ \dots\\ \end{align}$$

But isn't that just Dr. Loh's method?

Answer 8

Of course the final formula according to Loh's method should be the same as the usual quadratic formula because otherwise it would be wrong. But Loh's point is not to memorize a formula and simply plugin the coefficients. Rather, it's easier to find the answers through an algorithm. You can arrive at the same answer (roots of the quadratic equation) through different algorithms. Some algorithms are more efficient than others. Consider the two simple formulas, $ab+ac$ and $a(b+c)$. You get the same final answer either way. But the former has two multiplications and one addition whereas the latter has only one multiplication and one addition. So the latter is computationally more efficient.

For finding the roots of a quadratic equation, completing the square is one algorithm and Loh's method is another one. Given $x^2+bx+c=0$, Loh's method is to find the midpoint $m$ between the roots ($m = -b/2$) and the distance $d$ between the midpoint and a root ($d^2=m^2-c$). Notice that $d^2$ is calculated using $m$. When you have $m$ and $d$, you can finally get the roots: $x = m \pm d$. Loh's method is considerably efficient when $b$ is an even integer because then you don't have to deal with fractions unless $c$ is also fraction.