1

I am interested in finding linear recurrences for the number of n-step paths between two fixed vertices in a finite graph. The question is motivated by the same problem that led to this question.

For concreteness' sake, let's consider the graph $G$ on 16 vertices given by the adjacency matrix $$ M=\left( \begin{array}{cccccccccccccccc} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ \end{array} \right). $$

M={{1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0}, {0, 1, 1, 0, 0, 0, 
  0, 0, 0, 0, 0, 0, 0, 1, 1, 0}, {0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 
  0, 0, 0, 0}, {0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0}, {0, 
  0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 0, 0, 
  0, 0, 0, 0, 0, 1, 1, 0, 0}, {0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 
  0, 0, 0}, {0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0}, {0, 0, 
  0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 0, 0, 0, 
  1, 1, 0, 0, 0, 0, 0, 0}, {1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 
  0, 0}, {1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0}, {0, 0, 0, 
  0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0}, {1, 1, 0, 0, 0, 0, 0, 0, 0, 
  0, 0, 0, 1, 1, 0, 0}, {0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 
  0}, {1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1}};

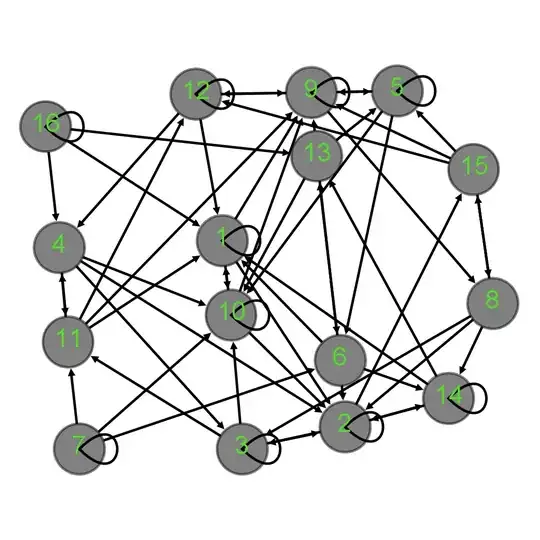
This directed graph has constant out-degree 4, some self-loops, und looks like this: Graph on 16 vertices

From counting paths in the graph directly, or computing powers of $M$, one finds that the numbers of $n$-step paths from $1$ to $1$ are given by

n      #paths      paths
-------------------------
1      1           1-->1
2      2           1-->1-->1, 1-->10--->1
3      6           1-->1-->1-->1, 1-->1-->10-->1, 1-->10-->1-->1, 1-->10-->10-->1, 1-->9-->12-->1, 1-->2-->14-->1
4      24
5      100
6      408
7      1640
8      6560
9      26224
10     104864
...    ...

Experimentally, we find that the number of $n$-step paths, $a_n$, satisfy the linear recurrence $$ a_n = 6\,a_{n-1} -10\,a_{n-2} + 8\,a_{n-3},\quad n>3, $$ e.g., for $n=4$, $$ 24 = 6\times 6 - 10\times 2 + 8\times 1 = 36-20+8=24. $$

Looking back from the end of an $n$-step path beginning and ending in $1$ it is clear that the number of such paths equals the sum of $(n-1)$-step paths beginning in $1$ and ending in any of the predecessors of $1$, that is in ${1,6,10,11,12,13,14,16}$, but from there things seem to get messy.

Similar recurrences, some of length 3, can be found for the number of $n$-step paths between any two vertices in this graph.

I believe that a simple random walk on this graph (with the sinks $7$ and $16$ removed) with uniform transition probabilities is an aperiodic irreducible Markov chain, and so counting the number of paths of terminating in a specific vertex would allow to compute the stationary distribution without solving an eigenvalue problem.

Questions:

1) Are linear recurrences between number of $n$-step paths a general feature of finite graphs or are their specific to this example?

2) What determines the order of the recursion?

3) How can one compute the coefficients in the recurrence? Is it easier or harder than (or incomparable to) solving the eigenvalue problem of $M$?

Eckhard
  • 7,705

1 Answers1

1

Too long for a comment.

First of all I assume you're counting "paths" where repeated nodes are allowed. I.e. the no. of $n$-step paths from $i$ to $j$ is simply the $(i,j)$ entry of $M^n$, which I will denote $M^n_{ij}$.

Let $v =$ no. of nodes, i.e. $M$ is size $v \times v$.

Since $M^n = M \times M^{n-1}$, we trivially have a system of $v^2$ recurrences: each recurrence expresses one of the $v^2$ values of $M^n_{ij}$ as a linear combination of the $v^2$ values of $M^{n-1}_{ij}$. (Each linear combo has at most $v$ non-zero terms, but I am not sure this helps.) Based on this alone, I'm 90% sure we can rewrite the recurrences s.t. each $M^n_{ij}$ is a linear combo of $M^k_{ij}$ where $k \in \{n-1, n-2, \dots, n-v^2\}$. I.e. by isolating each $(i,j)$ variable, you can get a recurrence in each $(i,j)$ variable that looks back at most $v^2$ steps in time. (I am only 90% sure this is doable, not 100%.)

Now of course in your case $v^2 = 16^2 = 256$, so this theoretical process (even if it works) does not explain how you can get recurrences in $M^n_{11}$ (what you called $a_n$) that looks back only $3$ steps in time.

Furthermore, I would think that if there is a path $i \to j$ that is e.g. $7$-hops long, then its contribution won't even show up until $n=7$. E.g. if the shortest $i \to j$ path is $7$-hops, then $M^n_{ij} = 0$ for $n < 7$, so no recurrence on $M^n_{ij}$ can look back fewer than $7$ time steps. Given your specific graph has many $1 \to 1$ paths that are quite long, I'm surprised you can write a recurrence that looks back only $3$ time steps.

antkam
  • 15,363
  • Thanks for the comment. Yes, repeated nodes are allowed in the path counting iff there is a self-loop at that node. I agree that the low order of the recurrence seems particularly surprising. – Eckhard Dec 27 '19 at 06:58
  • 1
    What do you mean repeated nodes are allowed iff there is a self loop? What about bigger loops? E.g. in your graph, $1 \to 10 \to 1 \to 10 \to 1$ should be a perfectly valid $4$-hop path even though no self-loop was used in that path. (And calculating based on $M^4$ would certainly include that path.) – antkam Dec 27 '19 at 07:02
  • Sorry, by "repeated node" I meant to refer to the same node being both the start and the end of a step in the path, such as 1-->1. I think we agree that an $n$-step path is just a sequence of not necessarily distinct nodes $v_{i_1},...,v_{i_{n-1}}$, such that $M_{i_j, i_{j+1}}=1$ for $j=1,...,n-1$. – Eckhard Dec 27 '19 at 07:37