Let
$$ H=\left(\begin{array}{cccc} 0 & 1/2 & 0 & 1/2 \\ 1/2 & 0 & 1/2 & 0 \\ 1/2 & 0 & 0 & 1/2\\ 0 & 1/2 & 1/2 & 0 \end{array}\right), $$
$K_1=\left(\begin{array}{c}1 \\ 0\end{array}\right)$ and consider the sequence of matrices defined by $$ K_L = \underset{2^{L}\times 2^{L}}{\underbrace{\left[H\otimes I_{2^{L-2}}\right]}}\underset{2^{L}\times 2^{L-1}}{\underbrace{\left[I_2 \otimes K_{L-1}\right]}}\in\mathbb{R}^{2^L\times 2^{L-1}}, $$ where $\otimes$ denotes the Kronecker product, and $I_n$ is the $n\times n$ identity matrix.
I am interested in the limiting behaviour of the singular values of $K_L$ as $L$ tends to infinity. Some calculations indicate that the $2^L\times 2^{L-1}$-matrix $K_L$ has $L$ non-zero singular values and that the empirical distribution of those nonzero singular values converges to some limit. Can this limit be described in terms of the matrix $H$?
I am wondering if it is possible to use some kind of fixed-point theorem to characterise the limit (in any sense) $\lim_{L\to\infty}K_L$ as an operator on some sequence space.
Edit: I did some more experiments and it seems that the limiting behaviour of the singular values of $K_L$ does not only depend on the matrix $H$, but also on the initial value $K_1$.
To illustrate this, let $K_1(\alpha)=\left(\begin{array}{c}1 \\ \alpha\end{array}\right)$ and consider the sequence $$ K_L(\alpha) = \left[H\otimes I_{2^{L-2}}\right]\left[I_2 \otimes K_{L-1}(\alpha)\right]. $$
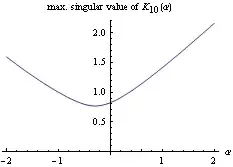
The largest singular value of $K_{10}(\alpha)$ is depicted in the following figure. (The graph looks essentially the same for all $L\geq 4$ instead of $L=10$.)
 $K_{10}(\alpha)$" />
$K_{10}(\alpha)$" />
The minimum is approximately $(-.2936,0.7696)$.
This makes it unlikely for fixed-point arguments to work in this setting. I, therefore, modify my question and ask if the limiting behaviour of the singular values of $K_L$ (or $K_L(\alpha)$) can be characterised directly in terms of $H$ and the initial value $K_1$ (or $K_1(\alpha)$).
Edit 2 (March 2015): As the question is still receiving attention, let me add that I came up with a conjecture for the asymptotic behaviour of the singular values of $K_L(\alpha),$ as detailed in this MO post.