I found this problem in some recreational mathematics textbook.
The given problem is as follows find the ratio of the colored triangle and entire triangle. [The number states the ratio]
The textbook simply states
and compute the area by counting triangles.
I realize in the process they treat following without proof.
i.e., the half of length of CD is one side of triangle.
From Geogebra manipulation I realized they are indeed same(marked length), but How one can prove this mathematically?
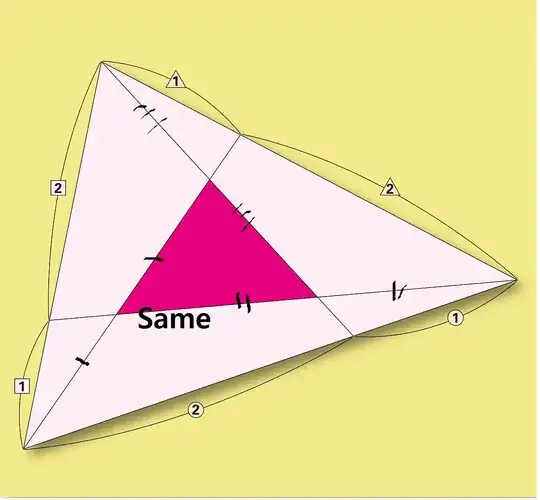
Let us restate, also introducing notations, so that there is nothing more to prove at the end.
Given is a triangle $\Delta ABC$. We consider intermediate points $A',A''\in BC$, $B',B''\in CA$, $C',C''\in AB$, so that $$ \frac{A'C}{BC} = \frac{B'A}{CA} = \frac{C'B}{AB} = \frac 13= \frac{BA''}{BC} = \frac{CB''}{CA} = \frac{AC''}{AB} \ . $$ The equidistant parallels
- to $AA'$ through $B,A'',A',C$ (one of them being $AA'$,
- to $BB'$ through $C,B'',B',A$ (one of them being $BB'$,
determine the points $X,X';Y,Y';Z,Z';S,T,U$ as in the following figure:
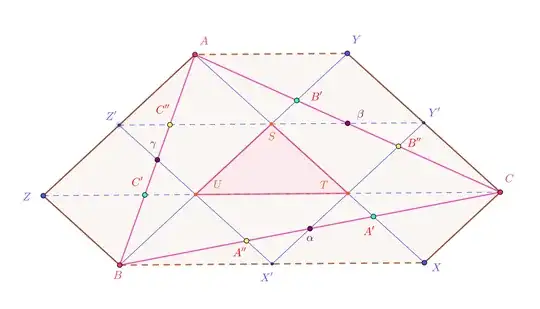We have also drawn the mid points $\alpha$, $\beta$, $\gamma$ of the sides of $\Delta ABC$ as orientation, but we do not need them.(Except for the Bonus.)
1.st Claim: The following quadrilaterals are congruent parallelograms: $AZ'US$, $Z'ZBU$, $YSTY'$, $SUX'T$, $Y'TXC$.
2.nd Claim: The following segments are parallel: $$ AY\ \|\ ZS\ \|\ SY'\ \|\ ZU\ \|\ UT\ \|\ TC\ \|\ BX'\ \|\ X'X\ \ . $$
In particular
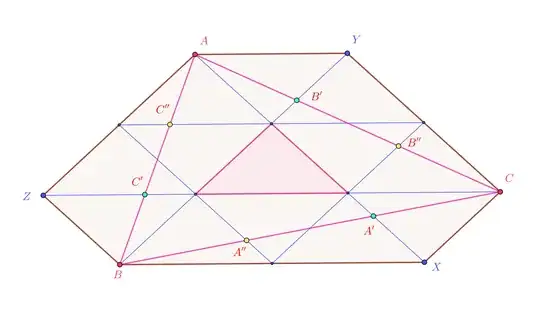
- the points $Z',C'',S,Y'$ (and $\beta$) are colinear,
- the points $Z,C',U,T,C$ are colinear,
- the points $B,X',X$ are colinear,
so that we can draw solid lines instead of the dotted lines:
The question in the OP follows now easily from the above construction. (The key word is equidistant parallels in all three directions.)
Proof: The first claim is clear, since we have two directions with three equidistant parallels in each one. The equidistance is insured by the fact that a intersecting line is delimited in equal segments, here explicitly $BA''=A''A'=A'C$ and $CB''=B''B'=B'A$.
For the second claim, we use the first one and succesively compare triangles built with one side parallel and congruent to $AZ'$, and an other one parallel and congruent to $AS$. We have for instance $\Delta AZ'S\equiv \Delta SYA$, because $AZ'$ is (via $US$) parallel and congruent to $SY$, adn $AS$ is a common side. This gives $AY\| Z'S$. (Congruence also holds for the two segments.) With a similar argument we add one by one the other segments in the parallel chain.
$\square$
Bonus: $\beta$ is for instance on $SY'$ and in fact its mid point, because it is the mid point of the one diagonal $AC$ in the parallelogram $ATCY$, so also of the other diagonal $YT$, which is also one diagonal in the parallelogram $YSTY'$.
Note: If we start with a lattice defined by two directions, make a choice of points $A,B,C$ as in the picture, and vectorially (for instance) also immediately accept that the "third direction works", there is nothing to be shown. But the question in the OP reduces to exactly this aspect. Also the above proof is easy, the only complicated thing is to make sentences that construct, and fix the known data step by step.
Two things :
1) About the equality of the lengths you are asking for, see the recent question Proof that each of the three cevians is divided in the ratio $1:3:3$ (with, among the answers, one of mine).
2) About the proportion ($1/7$) of areas :
Let $A,a$ be the resp. areas of the big and small (red) triangle.
In your second figure, the sum of the areas of the 12 (purple) copies of the initial triangle is $12a$.
This sum can be computed in a second manner by recognizing 3 parallelograms (one of them is $ABCD$) whose total area is the double of the area of the big triangle minus the area of the small triangle, giving the equation :
$$12a=2(A-a)$$
which amounts to :
$$a=\tfrac17A$$
Remarks :
1) The given figure can be connected to one of the figures one finds in this reference.
2) A generalization of the $1/7$ triangle is Routh theorem.
