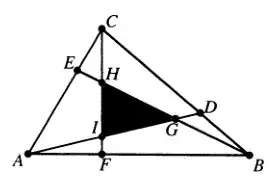
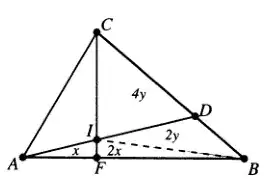
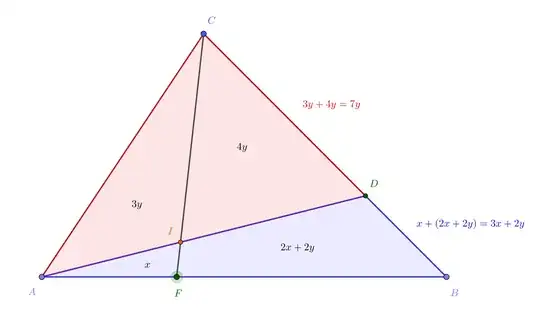
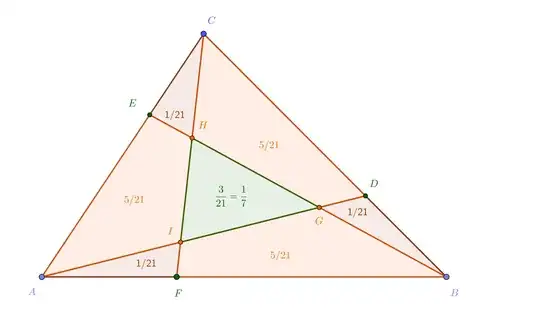
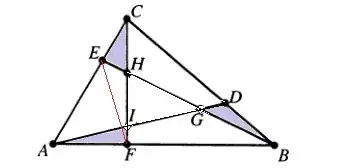
The use of areas and ratio of areas suggest that barycentric coordinates (also named areal coordinates) could be a rather systematic way to consider this issue.
Let us show in particular (it is equivalent to the (1:3:3) proportionnality) that
$$G=\tfrac47B+\tfrac37E \ \ \ (a) \ \ \ \ \text{and} \ \ \ \ H=\tfrac17B+\tfrac67E \ \ \ (b) \tag{1}$$
Normalized barycentric coordinates of $G$ and $H$ are shown (see Edit 1 below) to be :
$$G=[\tfrac17,\tfrac47,\tfrac27] \ \text{and} \ H=[\tfrac27,\tfrac17,\tfrac47] $$
As $B = [0,1,0]$ and $E = [\tfrac13,0,\tfrac23]$, checking (a) and (b) is immediate.
Edit 1 : Barycentric equations of
$$\begin{cases}\text{Line AD} &:& b-2c&=&0& B.C. : \{0,1,-2\}\\
\text{Line BE} &:& c-2a&=&0& B.C. : \{-2,0,1\}\\
\text{Line CF} &:& a-2b&=&0& B.C. : \{1,-2,0\}\end{cases}\tag{2}$$
where $B.C.$ denote (unnormalized) barycentric coordinates of the corresponding lines.
As is well known the barycentric coordinates of the crossing point of two lines are obtained as the cross product of their B.C.
Here, for example, the barycentric coordinates of $G=AD \cap BE$ are obtained by the cross product (see (2)) :$$ \{0,1,-2\} \times \{-2,0,1\}= (1,4,2)$$
which, under its normalized form, gives $[\tfrac17,\tfrac47,\tfrac27]$ for the barycentric coordinates of $G$, as awaited.
Edit 2 : Back to areas
There is a noteworthy application of barycentric coordinates : they provide easy calculations of areas. For example, the ratio (area of triangle GHI)/(area of reference triangle ABC) is equal to the determinant :
$$\det(G,H,I)=\begin{vmatrix}\tfrac17&\tfrac27&\tfrac47\\
\tfrac47&\tfrac17&\tfrac27\\
\tfrac27&\tfrac47&\tfrac17\end{vmatrix}=\frac17.$$
Connected... and interesting : https://en.wikipedia.org/wiki/One-seventh_area_triangle