3

Let a and b be the lengths of the semimajor and semiminor axes of an ellipse respectively.

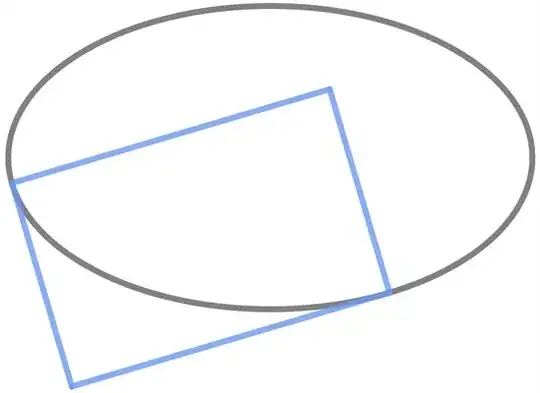
Draw a rectangle whose two sides are tangent to the ellipse and the other two are normal to the ellipse.

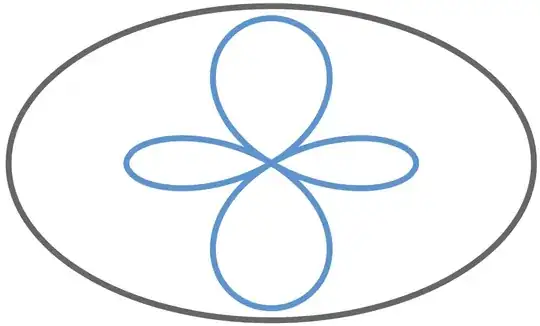
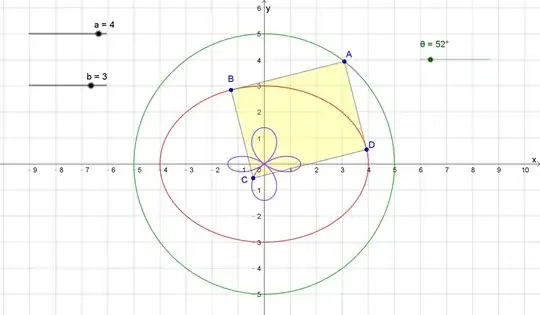
I want to find the area enclosed by the locus of the vertex of the rectangle at which the normals meet.

Ellipse and rectangle

Solution:-

My attempt:- We are required to find the locus of point $(h,k)$ from which two perpendicular lines can be drawn which are normal to the ellipse.

Normal to the ellipse at the point $(a \cos{\theta}, b\sin{\theta})$ is given by $ax\sec{\theta}-by\csc{\theta}=a^2-b^2$ and the slope of this normal is given by $m=\frac{a}{b}\tan{\theta}$

Now how to proceed futher?

Now by putting $x=h, y=k$ how to eliminate $\theta$ and write the equation in m?

And how to arrive at the final answer?

If any member knows the correct answer may reply with correct answer.

The graph of the vertex of the rectangle at which the normals meet provided to me is as follows

The graph of the vertex of the rectangle at which normals meet

Answer provided to me for the required area is $(a-b)^2\pi$

I tried to plot the equation provided in the comment section, in www.wolframalpha.com but it failed. see Here

Win_odd Dhamnekar
  • 1,056
  • It is probabily better to start observing that the rectangle vertex that lies outside the ellipse is on the so called orthoptic of the ellipse, which is a circumference with center in the origin of the axes, and with radius $\sqrt{a^2+b^2}$. This has a straightforward demonstration. Then, maybe, you can find the "corresponding" point inside the ellipse, working with polar coordinates as you started doing? – dfnu Dec 12 '19 at 20:09

1 Answers1

5

Let $A(u,v)$ be the outer vertex of the rectangle which should lies on the director circle, hence

$$u^2+v^2=a^2+b^2$$

Refer to another answer of mine here, the mid-point of the polar (the chord $BD$) is

$$\frac{1}{\dfrac{u^2}{a^2}+\dfrac{v^2}{b^2}} \begin{pmatrix} u \\ v \end{pmatrix}$$

Since diagonals bisect each others, the required locus for the inner vertex $C(x,y)$ is given by

$$ \begin{pmatrix} x \\ y \end{pmatrix}+ \begin{pmatrix} u \\ v \end{pmatrix}= \frac{2}{\dfrac{u^2}{a^2}+\dfrac{v^2}{b^2}} \begin{pmatrix} u \\ v \end{pmatrix} $$

Therefore $$ \begin{pmatrix} x \\ y \end{pmatrix}= \left( \frac{2}{\dfrac{u^2}{a^2}+\dfrac{v^2}{b^2}}-1 \right) \begin{pmatrix} u \\ v \end{pmatrix}$$

Converting into polar coordinates:

$$r^2=(a^2+b^2) \left( \frac{1-\dfrac{b^2\cos^2 \theta}{a^2}-\dfrac{a^2\sin^2 \theta}{b^2}} {1+\dfrac{b^2\cos^2 \theta}{a^2}+\dfrac{a^2\sin^2 \theta}{b^2}} \right)^2$$

enter image description here

The area can be found by using Mathematica: \begin{align} & \quad \frac{1}{2} \int_0^{2\pi} r^2 d\theta \\ &= 2(a^2+b^2) \int_0^{\tfrac{\pi}{2}} \left( \frac{1-\dfrac{b^2\cos^2 \theta}{a^2}-\dfrac{a^2\sin^2 \theta}{b^2}} {1+\dfrac{b^2\cos^2 \theta}{a^2}+\dfrac{a^2\sin^2 \theta}{b^2}} \right)^2 d\theta \\ & = 2(a^2+b^2) \left[ \theta- \frac{2ab}{a^2+b^2} \tan^{-1} \left( \frac{a\tan \theta}{b} \right)+ \left( \frac{2ab}{a^2+b^2} \right)^2 \frac{(a^2-b^2)\sin 2\theta}{a^2+b^2-(a^2-b^2)\cos 2\theta} \right]_0^{\tfrac{\pi}{2}} \\ & = \pi(a-b)^2 \end{align}

Addendum

By substituting $r^2=x^2+y^2$ and $(\cos \theta,\sin \theta)=\dfrac{(x,y)}{r}$, we have an implicit equation

$$(a^2+b^2)(x^2+y^2) \left( \frac{x^2}{a^2}+\frac{y^2}{b^2} \right)^2= (a^2-b^2)^2 \left( \frac{x^2}{a^2}-\frac{y^2}{b^2} \right)^2$$

which is consistent to another forum here.

Ng Chung Tak
  • 18,990