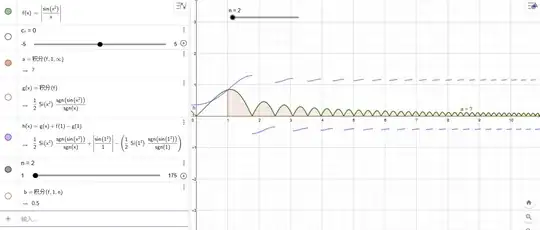
Proof for divergence of
$$
\newcommand{\abs}[1]{\left\vert #1 \right\vert}
\newcommand\rme{\mathrm e}
\newcommand\imu{\mathrm i}
\newcommand\diff{\,\mathrm d}
\DeclareMathOperator\sgn{sgn}
\renewcommand \epsilon \varepsilon
\newcommand\trans{^{\mathsf T}}
\newcommand\F {\mathbb F}
\newcommand\Z{\mathbb Z}
\newcommand\R{\Bbb R}
\newcommand \N {\Bbb N}
\renewcommand\geq\geqslant
\renewcommand\leq\leqslant
\int_1^{+\infty} \abs {\frac {\sin (x^2)}{x}} \mathrm dx.
$$
Easy to see $\abs {\sin (x^2)} \geq\sin^2 (x^2) = (1 - \cos (x^2))/2$ since $0 \leq \abs {\sin (u)} \leq 1$.
Then
$$
\int_1^{ +\infty } \frac {\abs {\sin (x^2)}}x \geq \frac 12 \int_1^{+\infty} \frac 1x \diff x - \frac 12 \int_1^{+\infty} \frac {\cos (2x^2)}x \diff x =: \frac 12( I_1 + I_2).
$$
Clearly $I_1$ diverges. For $I_2$, via the substitution $u = 2x^2$, or $x = \sqrt {u/2}$,
$$
I_2 = \int_2^{+\infty} \frac {\cos u} {\sqrt {u/2}} \diff \sqrt {u/2} = \int_2^{+\infty} \frac {\cos u} {2u} \diff u,
$$
and this is convergent by Dirichlet Test. Therefore the original integral is a sum of a divergent integral and a convergent integral, which shall be divergent as well.
Counterexample for integral test when the terms are not decreasing
Consider
$$
f(x) = \frac {\pi x} {1 + (\pi x)^6 \sin^2 (\pi x)}, x \geq 0.
$$
Then $f$ is nonnegative, and the limit $f(+\infty)$ does not exist, since $f (n) = \pi n \to +\infty$ as $n \to \infty$. Then the series $\sum_1^{+\infty} f(n)$ diverges since a necessary condition for convergence is that $\lim_{n \to +\infty} f(n) = 0$. But the integral $\int_0^{+\infty} f(x) \diff x$ converges since
$$
\int_n^{n+1} f(x) \diff x = \int_{n\pi}^{(n+1)\pi} \frac x {1 + x^6 \sin^2 x} \diff x\leq \frac {2\pi^2}{n^2},
$$
for each $n \in \N^*$, then the integral is bounded from above by $\pi^4/3$.