Calculus of variations: find $y(a/2)$ if $y(x)$ maximizes the volume of rotation

Question

A curve $y(x)$ of length $2a$ is drawn between the points (0,0) and (a,0) in such a way that the solid obtained by rotating the curve about the $x$-axis has the largest possible volume. Find $y\left(\frac{a}{2}\right)$.

Answer 1

Maximize $\displaystyle\int_0^a\pi y^2\,\mathrm{d}x$ while maintaining $\displaystyle\int_0^a\sqrt{1+y'^2}\,\mathrm{d}x=2a$. In other words:

find the $y$ so that $$ \int_0^a y\,\delta y\,\,\mathrm{d}x=0\tag{1} $$ for every $\delta y$ so that $$ \int_0^a\frac{y'\,\delta y'}{\sqrt{1+y'^2}}\,\mathrm{d}x=0\tag{2} $$ Integrating $(2)$ by parts gives $$ \int_0^a\frac{y''}{\left(1+y'^2\right)^{3/2}}\,\delta y\,\mathrm{d}x=0\tag{3} $$ $(1)$ and $(3)$ imply that there is a constant $b$ so that $$ -\frac{y''}{\left(1+y'^2\right)^{3/2}}=2b^2y\tag{4} $$ $(4)$ describes the critical $y$:

$\hspace{3.5cm}$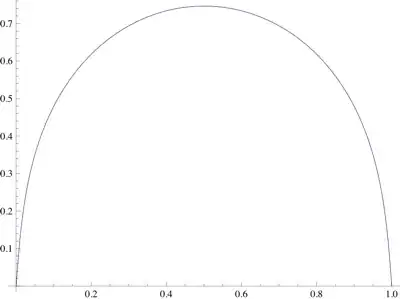

Multiply $(4)$ by $y'$, integrate, and solve for $y'$ $$ (1+y'^2)^{-1/2}=b^2y^2+c^2\\[6pt] y'=\pm\sqrt{\frac1{(b^2y^2+c^2)^2}-1}\tag{5} $$ Since $y''$ is always one sign, it must be negative. Thus, $y'$ is positive until $y$ reaches maximum, then it is negative until $y=0$.

The length of the curve is $$ \begin{align} &2\int_0^{\frac{\sqrt{1-c^2}}{b}}\sqrt{1+y'^2}\frac{\mathrm{dy}}{y'}\\ &=2\int_0^{\frac{\sqrt{1-c^2}}{b}}\frac{\mathrm{d}y}{\sqrt{1-(b^2y^2+c^2)^2}}\\[6pt] &=\frac{2\sqrt{1-c^2}}b\int_0^1\frac{\mathrm{d}y}{\sqrt{1-((1-c^2)y^2+c^2)^2}}\\ &=\frac2{b\sqrt{c^2+1}}\mathrm{EllipticK}\left(\frac{c^2-1}{c^2+1}\right)\tag{6} \end{align} $$ The width of the curve (distance between $x$-intercepts) is $$ \begin{align} &2\int_0^{\frac{\sqrt{1-c^2}}{b}}\frac{\mathrm{dy}}{y'}\\ &=2\int_0^{\frac{\sqrt{1-c^2}}{b}}\frac{(b^2y^2+c^2)\,\mathrm{d}y}{\sqrt{1-(b^2y^2+c^2)^2}}\\[6pt] &=\frac{2\sqrt{1-c^2}}b\int_0^1\frac{((1-c^2)y^2+c^2)\,\mathrm{d}y}{\sqrt{1-((1-c^2)y^2+c^2)^2}}\\ &=\frac2{b\sqrt{c^2+1}}\left((c^2+1)\mathrm{EllipticE}\left(\frac{c^2-1}{c^2+1}\right)-\mathrm{EllipticK}\left(\frac{c^2-1}{c^2+1}\right)\right) \tag{7} \end{align} $$ Solving for the $c$ that makes $(6)$ the double of $(7)$ yields $$ c=0.26829153853907013879\tag{8} $$ For that $c$, $(7)$ gives the width of the curve to be $$ a=\frac1b1.29027749675509851046\tag{9} $$ Equations $(4)$ and $(5)$ say that $y$ increases from $0$ to its maximum and returns to $0$ symmetrically. Thus, $y(a/2)$ is the maximum of $y$. Equation $(5)$ says that $y'=0$ when $$ y=\frac{\sqrt{1-c^2}}{b}\tag{10} $$ Answer: Therefore, combining $(8)$, $(9)$, and $(10)$ yields $$ y(a/2)=0.74661285489041830537\,a\tag{11} $$

---

Volume: Since we are maximizing the volume, why not compute the volume: $$ \begin{align} &2\int_0^{\frac{\sqrt{1-c^2}}{b}}\pi y^2\frac{\mathrm{dy}}{y'}\\ &=2\pi\int_0^{\frac{\sqrt{1-c^2}}{b}}\frac{y^2(b^2y^2+c^2)\,\mathrm{d}y}{\sqrt{1-(b^2y^2+c^2)^2}}\\[6pt] &=2\pi\left(\frac{\sqrt{1-c^2}}b\right)^3\int_0^1\frac{y^2((1-c^2)y^2+c^2)\,\mathrm{d}y}{\sqrt{1-((1-c^2)y^2+c^2)^2}}\\ &=\frac{2\pi\sqrt{c^2+1}}{3b^3}\left(\mathrm{EllipticK}\left(\frac{c^2-1}{c^2+1}\right)-c^2\mathrm{EllipticE}\left(\frac{c^2-1}{c^2+1}\right)\right) \tag{12} \end{align} $$ Combining $(8)$, $(9)$, and $(12)$ gives $$ \text{Volume}=1.21275710583444588043\,a^3 $$

Answer 2

Summary of my answer:

1. Some references for the classical isoperimetric problem of maximizing the area under a curve given a fixed arc length.

2. Reformulating the revoluted volume problem into a non-constraint optimization problem.

3. Example of why maximizing the revolution volume is not equivalent to maximizing the area under a curve given a fixed arc length.

4. Numerical approach and the approximation to $y(a/2)$ is $0.74a$ with the approximated maximized revoluted volume $1.212108 a^3$.

---

Let's say that the curve $y$ that maximizes the revolution volume subject to length $l$:

$$\text{Maximize }V[y] = \pi\int^a_0 y(x)^2\,dx\quad \text{subject to}\quad \int^a_0 \sqrt{1+\big(y'(x)\big)^2}\,dx = l.\tag{$\dagger$}$$

This is a modified version of the famous Dido's problem.

---

Isoperimetric approach for maximizing the AREA: If we allow the curve being defined as a parametric curve rather than a well-defined function's graph $(x,y(x))$, then the Isoperimetric theorem says:

The area surrounded by the straight line and a curve is maximum when the curve is a part of the circle with arclength fixed.

Similar argument could be made by a physical argument using membrane between ideal gas and vacuum, please refer to Mark's answer here. By the theorem, $$ y\left(\frac{a}{2}\right) = r(1-\cos\theta),\tag{A} $$ where $r$ and $\theta \in (0,\pi)$ satisfies: $$2r\theta = l,\quad \text{and}\quad 2r\sin\theta = a. $$ When $\theta = \pi/2$, it is a half circle and $l = \pi a/2$. When $l = 2a$, there exists a $\pi/2<\theta<\pi$, and $$ y\left(\frac{a}{2}\right) = \frac{a}{\theta}\left(1 + \sqrt{1-\frac{\theta^2}{4}}\right), \quad \text{where } \sin \theta = \frac{\theta}{2}. $$

---

Calculus of variation: If we are not allowed to have something like this. So we parametrize the curve $t\mapsto (x(s),y(s))$ for $s \in (0,l)$, so that $$ \int^a_0\sqrt{1+\big(y'(x)\big)^2}\,dx = \int^l_0 1 ds= l , \quad \text{and } (x')^2 + (y')^2 = 1. $$ Now $$ V[y] = \pi\int^a_0 y(x)^2\,dx = \pi\int^l_0 y^2 x'\,ds = 2\pi\int^l_0 y^2 \sqrt{1-(y')^2}\,ds. \tag{$\ddagger$} $$ Now the problem is transformed to an unconstraint problem, unfortunately the E-L equation is as follows: $$ 2y\sqrt{1-(y')^2} + \frac{d}{ds}\left(\frac{y^2 y'}{\sqrt{1-(y')^2}}\right) = 0.\tag{1} $$ Using another perturbation approach, letting $$\lim_{\epsilon\to 0}\frac{d}{d\epsilon} V[y+\epsilon v] =0$$ the variational problem is as follows: for any smooth $v$ $$ \int^l_0 \frac{2yv - 2y (y')^2 - y^2 y' v'}{\sqrt{1-(y')^2}} \,ds = 0.\tag{2} $$ Both (1) and (2) are subject to the boundary condition $y(0) = y(l) = 0$.

---

Equivalence?! No!

Question: Is problem $(\dagger)$ equivalent to $$\text{Maximize }A[y] = \pi\int^a_0 y(x)\,dx\quad \text{subject to}\quad \int^a_0 \sqrt{1+\big(y'(x)\big)^2}\,dx = l\,?$$

The answer is no. Let $l = \pi a/2$, then the largest area for a fixed arc length by formula (A) is achieved when $y$ is a half circle by the isoperimetric theorem: $$ y = \sqrt{\left(\frac{a}{2}\right)^2-\left(x-\frac{a}{2}\right)^2} \implies \frac{d}{dx}\frac{y'}{\sqrt{1+(y')^2}} = -\frac{d}{dx}\frac{x-a/2}{a/2} = -\frac{2}{a}.$$ So that the E-L equation of the Lagrange multiplier for maximizing the area under $y$ is satisfied. $$ 1-\frac{d}{dx} \frac{\lambda y'}{\sqrt{1+(y')^2}} =0, \quad \text{ where }\lambda = -\frac{a}{2}. $$ However, there does not exists any single $\lambda \in \mathbb{R}$ such that the E-L equation for the volume maximization problem holds if $y$ is a half-circle: $$ y-\frac{d}{dx} \frac{\lambda y'}{\sqrt{1+(y')^2}} =0. $$ According to WolframAlpha, equation of this kind should somehow involve the elliptic integral.

---

Numerical approach: After some furious trial and error for different functions satisfying the E-L equations for problem $(\dagger)$ and $(\ddagger)$, I am suggesting (as of now), a closed-form solution is impossible. So we turn to some numerical approach setting $a = 1$, $l=2$. Equi-distant sample points are: $(x_n,y_n)$, with $0\leq n\leq N+1$, step size $h$, $(x_0,y_0) = (0,0)$, and $(x_N,y_N) = (1,0)$.

Volume's approximation $V_h$ can be found by $$ V_h = \sum^{N}_{n=0}\pi h\frac{(y_n +y_{n+1})^2}{4} = \mathbf{y}^T A\mathbf{y}, $$ with $\mathbf{y} = (y_1,\ldots,y_n)$, and $A$ is a tri-diagonal matrix $$ A =\frac{\pi h}{4}\begin{pmatrix} 2 & 1 & & 0\\ 1 & \ddots & \ddots & \\ & \ddots & \ddots & 1 \\ 0 & & 1 & 2 \end{pmatrix}, $$ The arclength constraint is: $$ S_h = \sum^{N}_{n=0} \sqrt{(y_{n+1}-y_n)^2 + h^2} = 2. $$ This is a very hard nonlinear quadratic programming problem. Using $101\times 101$ grid points on $[0,1]^2$ (step size $h=10^{-2}$), $y(1/2)\approx 0.74$, blue curve is the curve maximizing the revoluted volume, while the red curve is a scaled circle that has the same arclength ($\mathrm{error}<O(10^{-2})$)

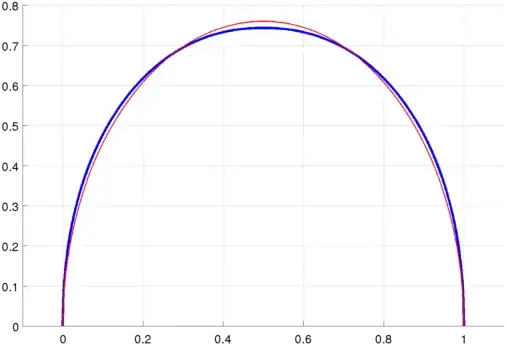
In computing the approximation, I found that the amount of work looking for all curves that satisfies the constraint is insanely large which is $O(2^{100})$! So here I admit I cheated the big way by assuming the following:

• The curve achives maximum at $x=1/2$, non-descreasing from $x=0$ to $x=1/2$, and is symmetric about $x=1/2$.

Hence now the problem turns into a pure integer programming, we want to find the increment step vectors for the first half $(v_1,\ldots,v_{N/2})$, with each entry non-negative. The curve's $y$-coordinates can be then written as the following with a lower-triangular matrix $B$:

$$ \begin{pmatrix}y_1\\ \vdots \\y_{N/2} \end{pmatrix} =h\begin{pmatrix} 1 & 0 & 0& 0\\ 1 & 1 & \ddots & 0\\ 1& \ddots & 1 & 0 \\ 1 &1 & 1 & 1 \end{pmatrix}\begin{pmatrix}v_1\\ \vdots \\v_{N/2} \end{pmatrix}. $$ Let $v = (v_1,\ldots,v_{N/2},v_{N/2},\ldots,v_1)^T$, then $$ y = \begin{pmatrix}B & 0\\ E & -B \end{pmatrix}v = Cv, $$ where $E$ is a matrix with all its entries being $1$. Notice the boundary condition is already incorporated for we consider only the increment (we can set $v_0 = 0$), now the problem changes to:

$$\text{Maximize } V_h[v]= v^T C^T ACv \\ \text{subject to } v_n \geq 0, \sum^{N/2}_{n=1} v_n \leq N,\;\text{and } S_h[v] = \sum^{N/2}_{n=0} 2h\sqrt{ v_n^2 + 1} = 2. \tag{$\star$}$$

In real simulation, I used Monte Carlo for $(\star)$ (I am not an expert in nonlinear optimization, there should be a more state-of-art approach rather than this brute force approach). The numerical procedures roughly are:

1. Generating an enormous amount of random numbers in scaled Dirichlet distribution for integer (non-negative numbers with sum fixed) with a fixed sum from $N-1,N-2,\ldots, N/2$. This fixed sum is the total number of steps $y$ goes up in the grids from $x=0$ to $x=1/2$. Notice $N/2$ is the highest number of increment steps in a perfect circle, for the arclength is $2>\pi/2$ so we wanna at least choose increment step more than that heuristically, unless there exists some zig-zag curves that maximize the volume (zig-zag won't pass the arclength constraint though).

2. Checking which increment step vectors are satisfying the arclength constraint within certain relative error $\epsilon$ (I chose $0.05$ in simulation).

3. Compute the volume then choose the maximum one.

4. Decreasing the $\epsilon$ for the arclength, perturb the increment step vector, repeat.

The eventual $y(1/2)= h\sum_{n=1}^{N/2} v_n$ for that maximizer increment step vector. What I got was $$ y(1/2)\approx 0.74, \text{ with } V[y] \approx 1.212108. $$

---

Lastly the problem reminded me of a youtube video long time ago: Using soap bubble to find the Steiner points for four fixed nodes.

Answer 3

When rotating about $x-axis$ maximum volume is equal to maximum area in 2D. Therefore the question can be given as max area given the length. The area to be maximized can be defined as

$$A[y]=\int_{x_1}^{x_2}y\ dx$$ subject to $$2a=\int_{x_1}^{x_2}\sqrt{1+y'\ ^2} dx$$

We can use Lagrange multiplier such as

$$H=y+\lambda \sqrt{1+y'\ ^2}$$ and $$\frac{\partial H}{\partial y}-\frac{d}{dx}\bigg(\frac{\partial H}{\partial y'}\bigg)=0$$ $$1-\frac{d}{dx}\bigg(\frac{\lambda y'}{\sqrt{1+y'\ ^2}}\bigg)=0$$ $$\Rightarrow \frac{x-\alpha}{\lambda}=\frac{y'}{\sqrt{1+y'\ ^2}}$$ If $\bar x=x-\alpha$ $$\frac{\bar x}\lambda=\frac{y'}{\sqrt{1+y'\ ^2}}\Rightarrow y'=\frac{dy}{dx}=\frac{\bar x}{\sqrt{\lambda^2-\bar x^2}}$$ which can be solved for $y(x)$ such that $$y(x)=-\sqrt{\lambda^2-\bar x^2}+\beta=\beta-\sqrt{\lambda^2-\big(x-\alpha\big)^2}$$ The equation must satisfy following conditions $$(0,0)\Rightarrow 0=\beta-\sqrt{\lambda^2-\big(-\alpha\big)^2}$$ $$(a,0)\Rightarrow 0=\beta-\sqrt{\lambda^2-\big(a-\alpha\big)^2}$$ $$2a=\int_{0}^{a}\sqrt{1+y'\ ^2} dx\qquad y'=\frac{x-\alpha}{\sqrt{\lambda^2-\big(x-\alpha\big)^2}}$$ which you can solve to find $\alpha$, $\beta$ and $\lambda$. From $(0,0)$ condition it follows that $$\beta=\sqrt{\lambda^2-\big(\alpha\big)^2}$$ By replacing it into $(a,0)$ condition it follows that $\alpha=a/2$. We can rewrite the equation as a circle equation $$\bigg(y-\sqrt{\lambda^2-\big(a/2\big)^2}\bigg)^2+\bigg(x-a/2\bigg)^2=\lambda^2$$

---------------EDIT-------------------

Although it produces a nice result; the equation is wrong. It assumes that every $dA$ produces the same amount of $dV$. It would have been right when the volume was produced by extrusion; but in rotational case $dA$ away from axis produces bigger $dV$.