5

Without calculator, how to prove that $2 \sqrt{3} > \pi$?

The level is baccalauréat grade. I confirm it's not a school exercise at all, as I left school like 35 years ago.

Michael Hardy
  • 1
TiLapiot
  • 99
  • 4
  • 4
    Welcome to MSE. Your question is phrased as an isolated problem, without any further information or context. This does not match many users' quality standards, so it may attract downvotes, or be put on hold. To prevent that, please [edit] the question. This will help you recognise and resolve the issues. Concretely: please provide context, and include your work and thoughts on the problem. These changes can help in formulating more appropriate answers. – José Carlos Santos Nov 26 '19 at 06:55
  • 2
    If you know that $\sqrt 3 \approx 1.732$ and $\pi \approx 3.1416$ you don't need a calculator – Ross Millikan Nov 26 '19 at 06:57
  • 10
    The perimeter of a circumscribed hexagon of the unit circle is $4\sqrt3$, while the perimeter of the circle, which is clearly smaller, is $2\pi$. – Rushabh Mehta Nov 26 '19 at 07:00
  • 4
    @DonThousand "clearly"? Clearly a word to avoid in maths. – Jean-Claude Arbaut Nov 26 '19 at 07:01
  • 4
    @Jean-ClaudeArbaut I'm offering a sketch. I'm not submitting an answer ... Clearly is perfectly appropriate in sketching proofs. – Rushabh Mehta Nov 26 '19 at 07:02
  • 2
    @DonThousand The problem is, it's not that clear here, especially at that level. – Jean-Claude Arbaut Nov 26 '19 at 07:03
  • 1
    @Jean-ClaudeArbaut Are you telling me that the fact that the perimeter of a regular polygon circumscribed around the circle is greater than the perimeter of the circle is not clear to prove? At this level? – Rushabh Mehta Nov 26 '19 at 07:04
  • 2
    baccalauréats are, what, 18? Ross and Don's arguments would both be clear to students when they first learn trig. –  Nov 26 '19 at 07:08
  • 1
    I disagree. But that's not important. See https://math.stackexchange.com/questions/2581157/polygon-circumscribed-about-circle-has-higher-perimeter-than-circle Rectifiable curves are not common at 18 (at least in France). – Jean-Claude Arbaut Nov 26 '19 at 07:11
  • 2
    @DonThousand Actually, Jean-Claude may have a point. It's trivial enough to show that an inscribed polygon has a smaller perimeter than its circumcircle (because "everyone knows" that a straight line segment is the shortest distance between two points on the plane). But for a circumscribing polygon, the situation is trickier. Maybe my brain is not functioning right now, but I can't see an elementary (no analysis) way to conclude that the perimeter of the polygon is strictly larger than the circumference of the incircle. (Enclosed area is much easier to "see" immediately in both cases). – Deepak Nov 26 '19 at 07:15
  • 2
    The area argument is immediately convincing and neater. – Deepak Nov 26 '19 at 07:28
  • 1
    There’s that nice integral that shows pi<22/7. All that remains to show is that 2\sqrt3>22/7, or 14\sqrt3>22, which can be seen by squaring both sides: 588>484. – G Tony Jacobs Dec 03 '19 at 06:03
  • A seemingly dry question - but I really like the neat answers it has triggered. Voted to reopen. But what to change to meet standards of MSE? Perhaps adding tag "recreational"? Or "proofs-without-words"? Or...? – Gottfried Helms Dec 05 '19 at 01:53

6 Answers6

19

enter image description here

(Credit to David G. Stork for the image).

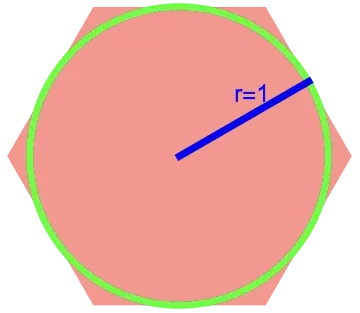
I am showing the area-based argument explicitly because it seems that the other answers rely on a perimeter-based argument (which I find unconvincing without a rigorous proof). In contrast, it is quite easy to conclude by simple inspection that the circumscribed hexagon has a larger area than the inscribed circle.

The area of the circle is clearly simply $\pi$.

The hexagon can be decomposed into six congruent equilateral triangles. The height of each is $1$. The base can be computed with trigonometry as $(2)\tan\frac{\pi}{6} = \frac 2{\sqrt 3}$. Hence the area of a single triangle is $\frac 12 (1)(\frac 2{\sqrt 3})= \frac 1{\sqrt 3}$. The area of the hexagon is therefore $\frac 6{\sqrt 3} = 2\sqrt 3$.

This allows us to immediately conclude $2\sqrt 3> \pi$ as required.

Deepak
  • 26,801
  • Sorry, I was not clear. I just meant, for geometric proofs what one considers "unconvincing without a rigorous proof" vs "quite easy to conclude by simple inspection" is rather subjective. – philipxy Dec 08 '19 at 00:00
  • 1
    @philipxy Fair enough. It is subjective. But if you consider that even a child can draw a very squiggly curve inside a circle, with the squiggly curve having a greater perimeter than the enclosing circle, the issue becomes clearer. You have to bring in the notion of convexity to make the argument convincing in the case of the perimeter, and showing it properly relies on things like Crofton's formula (which are in the realm of analysis). Whereas even with the squiggly curve, the area argument remains visually obvious. I hope you can see this too. It's not all that subjective after all. – Deepak Dec 08 '19 at 01:30
  • It is extremely difficult to prove anything geometrically non-analytically. (And when the question is analytic in the first place it adds a pile of unnecessary weight.) It's very easy to suggest with a diagram; but a suggestion is not a proof. Little is clear or obvious; much is merely plausible, and when so, not the general case. PS Anyway, when people ask for proofs they need to say what they accept as given, or the question is ill-defined and/or trivial--take your pick(s)--and indeed what they even mean by "prove". – philipxy Dec 15 '19 at 04:57
15

By a geometric argument just consider a circle inscribed in an hexagon and compare the two perimeters to obtain

$$3 \cdot \frac23 \sqrt 3 > \pi \cdot 1 \iff 2\sqrt 3>\pi$$

enter image description here

user
  • 154,566
12

We know that $\tan x \gt x$ for $x\in (0,\frac{\pi}{2})$. So, when $x = \frac{\pi}{6}$

$\tan \frac{\pi}{6} \gt \frac{\pi}{6} \implies \frac{1}{\sqrt3} \gt \frac{\pi}{6} \implies 2\sqrt3 \gt \pi$

Martin Sleziak
  • 53,687
Prabath Hewasundara
  • 1,644
11

Consider the perimeters in this figure:

enter image description here

$$2 \pi < 4\sqrt{3}$$

David G. Stork
  • 29,774
  • 2
    Nice diagram. As I commented, I think the perimeter argument is a bit cleaner since the numbers work out exactly. But this is, in my opinion, the best approach. – Rushabh Mehta Nov 26 '19 at 07:12
  • The most practical proof! – Sujit Bhattacharyya Nov 26 '19 at 07:14
  • 1
    Now you have to prove that the circumscribed polygon has a larger perimeter, which, as "obvious" as it may seem, is not that trivial. See https://math.stackexchange.com/questions/2581157/polygon-circumscribed-about-circle-has-higher-perimeter-than-circle – Jean-Claude Arbaut Nov 26 '19 at 07:14
  • @Jean-ClaudeArbaut If you are so bothered by the perimeter argument, the area argument works basically the same way. The perimeter argument simply relies on polygons being convex (and circles also being convex). – Rushabh Mehta Nov 26 '19 at 07:18
  • 3
    The area argument is neater and more convincing for elementary level students (all that's needed is a bit of trigonometry). But this answer appears to use a perimeter argument (the area argument immediately yields the required inequality without any cancellation needed). – Deepak Nov 26 '19 at 07:28
  • @DavidGStork I hope you don't mind that I've added an answer with the area argument explicitly given using your image as a reference. Let me know if you have an issue with it and I'll replace the image. Thanks. – Deepak Nov 26 '19 at 07:41
  • 1
    @Deepak: Oh... it is fine. Thanks for the credit. – David G. Stork Nov 26 '19 at 18:29
  • @DavidG.Stork In your edit, you changed $\frac{12}{\sqrt{3}}=6.9$ to $\frac{4}{\sqrt{3}}=2.3$, which made the inequality false. I believe you meant to change it to $4\sqrt{3}=6.9$. – Jam Nov 28 '19 at 19:03
1

Let us consider an equilateral triangle of side length $a$. The area of equilateral triangle is $$A_e=\frac{\sqrt3a^2}{4}$$ Let there be incentre in the triangle. Incentre Radius $$r=\frac{a}{2\sqrt3}$$ Area of circle $$A_c=\pi r^2 = \frac{\pi a^2}{12}$$ Since $$A_e>A_c$$ $$\frac{\sqrt3a^2}{4} > \frac{\pi a^2}{12}$$ $$3\sqrt3>\pi$$

If you consider a circle in a square, then $$a^2>\pi a^2/4$$ $$4>\pi$$

If you consider a circle in hexagon then $$\frac{3\sqrt3 \cdot a^2} 2 > \pi\left(\frac{\sqrt3}2\cdot a \right)^2$$ $$2\sqrt3>\pi.$$

In general, incentre Radius of a circle inscribed in a polygon of side $n$ and length $a$ is $$\frac{a}{2\tan{180^\circ/n}}$$

Michael Hardy
  • 1
Bijay
  • 384
1

Noting the fact that $$\tan\theta \geq \theta~~\forall x\in\left[0,\frac\pi2\right)$$ with equality for $x=0$

we have $$\tan\frac\pi6>\frac\pi6$$ $$\implies \frac{\sqrt 3}3 >\frac\pi6$$ $$\implies \sqrt3 >\frac\pi2$$ $$\implies\boxed{2\sqrt3>\pi}$$

Certainly not a dog
  • 1,452