How to prove this inequality(7)?

Question

Let $x,y,z\in\mathbb{R}$, prove that $$4(x^6+y^6+z^6)+5(x^5y+y^5z+z^5x)\ge\dfrac{(x+y+z)^6}{27}$$

I do this sometimes, and I think this problem is very hard, I hope someone can solve. Thank you.

By this way: In china BBs: Have solve this follow equality $$4(x^6+y^6+z^6)+5(x^5y+y^5z+z^5x)\ge 0$$ for $x,y,z\in R$ see:

http://www.aoshoo.com/bbs1/dispbbs.asp?boardid=48&id=24626&authorid=0&page=3&star=1

Answer 1

The following proof is rather more computational than I'd have liked. This seems hard to avoid, because the inequality $$ a(x^6+y^6+z^6) + b(x^5 y + y^5 z + z^5 x) \geq 3(a+b) \left(\frac{x+y+z}{3}\right)^6 $$ becomes false if the coefficient ratio $b/a$ is increased from $1.25$ to $1.33$ (try $(x,y,z) = (6,11,-10)$). On the bright side, the technique applies to many other such inequalities.

For $x,y,z \in {\bf R}$ let $$ F(x,y,z) = 4(x^6+y^6+z^6) + 5(x^5 y + y^5 z + z^5 x) - \frac{(x+y+z)^6}{27}. $$ We claim that $F(x,y,z) \geq 0$, with equality if and only if $x=y=z$. By homogeneity and cyclic symmetry we may assume $x=1$ and write $(x,y,z) = (1,1,1) + (0,c,rc)$ for some real $c,r$. [If $y=1$ and $z\neq 1$ we can use the equivalent $(1,1,1) + (rc,0,c)$.] Fixing $r$, we see that $F(x,y,z)$ is a sextic in $c$ with a double root at $c=0$, so we may write $$ F(1,1+c,1+rc) = c^2 Q_r(c) $$ for some quartic $Q_r$. We claim that $Q_r(c) > 0$ for all real $c$. For any given $r$, say $r=0$, this is easy to check by observing that $Q_r(c) > 0$ (for example $Q_0(c) > 65$) and computing the complex roots of $Q_r$ to enough precision to ensure that none of them is real. Now as we vary $r$, the roots must stay non-real as long as they are distinct (because they vary continuously with $Q_r$, which varies continuously with $r$). Well, the discriminant of $Q_r$ with respect to $c$ is a somewhat complicated polynomial $P(r)$, of degree $24$, which however is still small enough to compute all of its complex roots. It turns out that none of them is real either (the smallest imaginary parts are about $\pm 0.11$). Therefore $Q_r$ has distinct roots for all $r \in {\bf R}$, and we are done.

[$P$ is a bit simpler than its degree and coefficient size indicate: the cyclic symmetry of $F$ is inherited by $P$, which satisfies $P(r) = r^{24} P(\frac{r-1}{r})$; NB applying the fractional linear transformation $r \mapsto \frac{r-1}{r}$ three times returns $r$. So we can write $$ \frac{P(r)}{(r-r^2)^8} = P_1\Bigl(\frac{1-3r+r^3}{r-r^2}\Bigr) $$ for some polynomial $P_1$ of degree $8$. But this $P_1$ is still too long to fit in a single-line formula: it is $5^3/3^9$ times the polynomial whose coefficients (listed from leading to constant) are 65402051, 380534982, 2948475267, 8118916470, 30806414100, 47234529054, 159944730867, 165184306830, 420238105803. Here the imaginary parts of the roots are about $\pm 2.06$, $\pm 2.33$, $\pm 2.52$, $\pm 4.35$, all safely far from zero.]

Answer 2

Definition: $$ f(x,y,z) = 4(x^6+y^6+z^6) + 5(x^5 y + y^5 z + z^5 x) - \frac{(x+y+z)^6}{27} $$ We have to prove that $\;f(x,y,z) \ge 0\;$ for all $\;x,y,z \in {\bf R}$ .
For $\;x=y=z=r\;$ equality holds: $\;f(r,r,r)= 12 r^6 + 15 r^6 - (27^2 r^6)/27 = 0$ .
As has been noticed by user64494, the problem is invariant for scaling the variables with a factor $t$ : if the statement is true for $(x,y,z)$ then it is true for $(t x,t y,t z)$ as well. Meaning that, without loss of generality, we can consider instead only normed solutions, with $t=1/\sqrt{x^2 + y^2 + z^2}$. That is: with $x=y=z=0$ as the only exception. Note, however, that we have already covered this case with $f(r,r,r)=0$ where $r=0$ . Therefore WLOG we can define an additional constraint $\,g\,$ for all $(x,y,z)$ with $(x \ne 0) \vee (y \ne 0) \vee (z \ne 0)$ : $$ g(x,y,z) = x^2 + y^2 + z^2 = 1 $$ In my answer to a similar question, the following key reference is mentioned:

• Do symmetric problems have symmetric solutions?

From this reference we have (again) the following
Theorem (The Purkiss Principle). Let $f$ and $g$ be symmetric functions with continuous second derivatives in the neighborhood of a point $P = (r, \cdots, r)$. On the set where $g$ equals $g(P)$, the function $f$ will have a local maximum or minimum at $P$ except in degenerate cases.
The functions $\;f(x,y,z)\;$ and $\;g(x,y,z)\;$ have already been defined accordingly.
Now $\;g(r,r,r) = 3r^2 = 1$ , hence the point $P\;$ is: $(r,r,r) = (1,1,1)/\sqrt{3}\;$ and $\;f(r,r,r) = 0\;$ must be a minimum or a maximum.
It's easy to show that the first and second derivatives of $f$ and $g$ are like the examples in the paper - preceding the proof of the Theorem there; and obeying all of the Lemmas there - thus preventing any exceptions to the Purkiss principle.
First order derivatives: $$ \left[ \begin{array}{c} \partial f / \partial x \\ \partial f / \partial y \\ \partial f / \partial z \end{array} \right] (r,r,r) = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right] = \lambda \left[ \begin{array}{c} \partial g / \partial x \\ \partial g / \partial y \\ \partial g / \partial z \end{array} \right] (r,r,r) = 0 \left[ \begin{array}{c} 2 r \\ 2 r \\ 2 r \end{array} \right] $$ Second order derivatives: $$ \left[ \begin{array}{ccc} \partial^2 f/\partial x^2 & \partial^2 f/\partial x \partial y & \partial^2 f/\partial x \partial z \\ \partial^2 f/\partial x \partial y & \partial^2 f/\partial y^2 & \partial^2 f/\partial y \partial z \\ \partial^2 f/\partial x \partial z & \partial^2 f/\partial y \partial z & \partial^2 f/ \partial z^2 \end{array} \right] (r,r,r) = \left[ \begin{array}{ccc} 130 r^4 & -64 r^4 & -64 r^4 \\ -64 r^4 & 130 r^4 & -64 r^4 \\ -64 r^4 & -64 r^4 & 130 r^4 \end{array} \right]$$ Similar structure, as required, in: $$ \left[ \begin{array}{ccc} \partial^2 g/\partial x^2 & \partial^2 g /\partial x \partial y & \partial^2 g/\partial x \partial z \\ \partial^2 g/\partial x \partial y & \partial^2 g/\partial y^2 & \partial^2 g/\partial y \partial z \\ \partial^2 g/\partial x \partial z & \partial^2 g/\partial y \partial z & \partial^2 g/ \partial z^2 \end{array} \right] (r,r,r) = \left[ \begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{array} \right] $$ The form of the second order derivatives matrices guarantees that $\;f(r,r,r)\;$ must be a minimum.

Update in response to the comment by David Speyer.
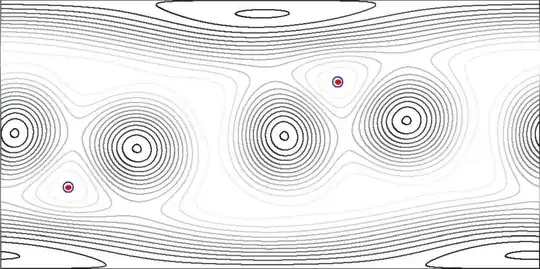
Due to the constraint $x^2+y^2+z^2=1$ the whole problem can be re-formulated in spherical coordinates: $(x,y,z)=(\cos(\theta)\cos(\phi),\cos(\theta)\sin(\phi),\sin(\theta))$ with $-\pi/2<\theta<+\pi/2$ and $-\pi<\phi<+\pi$ . Substitute these into $f(x,y,z)$ and make a contour plot $(\phi,\theta)$ . We have done this for $f(x,y,z) = k/3 \; , \; k = 1,\cdots\,15$ . Darker lines correspond with larger values of $f$ . Places where $f(x,y,z) < 0.01$ are colored $\color{red}{red}$ and the places of the minima $\;\pm 1/\sqrt{3}(1,1,1)\;$ in spherical coordinates are indicated with a $\color{blue}{blue}$ circle. We see that the circles and the red spots coincide and that the function values are uniformly decreasing in the neighborhood of these.