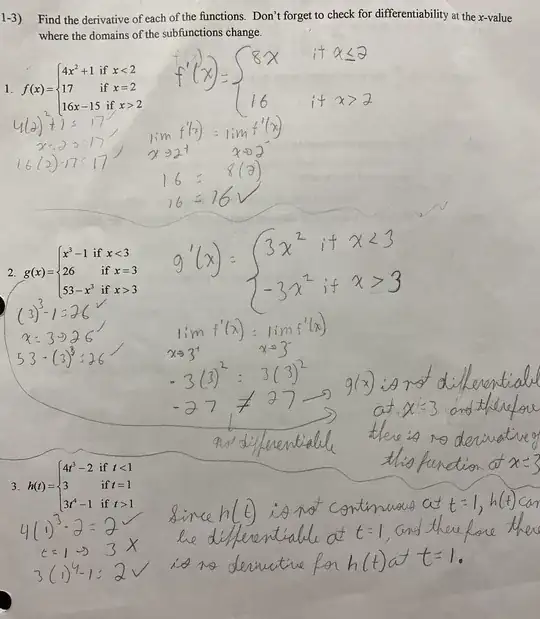For problems 2 and 3 attached, I have found that for problem 2 that the piecewise function is not differentiable at x=3, but I was wondering if there could still be a derivative that can be written. I thought that there is no derivative, but now I am looking back at this problem and I am quite unsure. Also for problem 3, I found that the piecewise function is not continuous at t=1. Therefore, I concluded that the function is not differentiable at t=1 and therefore there is no derivative for the piecewise function. Am I wrong here?
-
if a function isn't continuous at a point it cannot be differentiable in the usual sense of the word at that point; you can however take the limit of the derivative and approach the "problematic" point from either side: that way you get two possible derivatives that don't correspond with each othe mos of the time. That's not what we usually mean when we ask if a function is differentiable at a point though. – sortai Oct 29 '19 at 22:57
-
So what you are saying is that for problems 2 and 3 a derivative exists? – P1081 Oct 29 '19 at 23:06
-
no, the derivative isn't defined at that point – sortai Oct 29 '19 at 23:07
-
So my answers were correct? Sorry, I'm just trying to make sure I understand this correctly. – P1081 Oct 29 '19 at 23:08
-
yes, you are correct. Sorry if I made it more complicated than it needed to be – sortai Oct 29 '19 at 23:10
-
1Thank you for your help! – P1081 Oct 29 '19 at 23:11
1 Answers
Differentiability and existence of derivative at a point are two equivalent concepts. Notably we say that the derivative at a point $x_0$ exists when the following limit exists finite
$$\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}$$
this definition is equivalent to the differentiability for $f(x)$ at $x_0$ that is exists $L\in \mathbb R$ such that
$$f(x+x_0)=f(x_0)+L(x-x_0)+o(x-x_0)$$
and we can show that $L=f'(x_0)$.
In your case, for problem $2$
$$\lim_{x\to 3^+}\frac{g(x)-g(3)}{x-3}\neq \lim_{x\to 3^-}\frac{g(x)-g(3)}{x-3}$$
and therefore by definition the function $g(x)$ is not differentiable at $x=3$.
The same result can be obtained evaluating $g_1'(x)$ for $x>3$ and $g_2'(x)$ for $x<3$ and observing that
$$\lim_{x\to 3^+}g_1'(x) \neq \lim_{x\to 3^-}g_2'(x)$$
Refer for that way also to: Prove that $f'(a)=\lim_{x\rightarrow a}f'(x)$..
For problem $3$ since $h(t)$ is not continuous at $t=1$ it is not differentiable at that point and then neither the derivative exists.
- 154,566