2

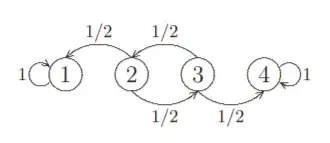
Let's consider the following Markov chain. If we start at state $2$, compute the probability to hit $4$ and the expected time until it happens.

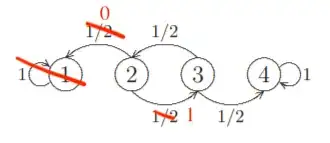
enter image description here

The probability to hit $4$ in $n$ steps starting at $2$ is $Pr(X_n=4|X_0=2)=(\frac{1}{2})^n$ if $n$ is even, and $0$ if $n$ is odd. Then, the total probability of hitting 4 if we start at 2 will be$\sum_{n\geq1}Pr(X_n=4|X_0=2)=\sum_{i\geq1}(\frac{1}{2})^{2i}=\sum_{i\geq1}\frac{1}{4^i}=\frac{1}{3}$

How can I calculate $\mathbb{E}(T_{24})?$ I have tried considering the mean hitting times $m_{ij}$, so $m_{24}=1+\frac{1}{2}m_{14}+\frac{1}{2}m_{34}$ and $m_{34}=1+\frac{1}{2}m_{44}+\frac{1}{2}m_{24}=1+\frac{1}{2}m_{24}$.

The solution in my book is $m_{24}=m_{34}=3$, which does not seem intuitive to me.

Community
  • 1
Gibbs
  • 544
  • Your intuition is good. To get to state 4 from state 2, the system must always go through 3, so it would be highly surprising for the mean absorption times to be the same. – amd Oct 20 '19 at 18:06

2 Answers2

2

I get $m_{24}=4$ and $m_{34}=3$. We are computing the expected time to hit state $4$ starting in state $2$, assuming that it happens. There is a positive probability that we never reach state $4$ so if we don't condition the expectation on success, it would be $\infty.$

Therefore, we have to adjust the state diagram. The arrow from state $2$ to state $1$ goes away, and the arrow from state $2$ to state $3$ gets weight $1$. Now we have $$\begin{align} m_{24}&=1+m_{34}\\ m_{34}&=1+\frac12 m_{24} \end{align}$$ which leads to the solutions I gave above. You may find the accepted answer to Expected time till absorption in specific state of a Markov chain instructive.

saulspatz
  • 53,131
0

The general way for computing mean hitting times of any absorbing state is well known, rather easily proven and in this Wikipedia article.

To get the mean hitting time of a specific state (or subset of states), we simply condition the outcome on hitting that state. For this question, the modified chain looks like:

enter image description here

This gives us the transition matrix $\Pi$, where $\Pi_{ij}$ gives the probability of transitioning to state j from state i:

$$ \begin{pmatrix} 0 & 1 & 0\\ \frac{1}{2} & 0 & \frac{1}{2}\\ 0 & 0 & 1 \end{pmatrix} $$

And Q: $$ \begin{pmatrix} 0 & 1 \\ \frac{1}{2} & 0 \end{pmatrix} $$

So that $$ \begin{align} m &= (I-Q)^{-1}1 \\ &= \begin{pmatrix} 2 & 2 \\ 1 & 2 \end{pmatrix}1 \\ &= \begin{pmatrix} 4 \\ 3 \end{pmatrix} \end{align} $$

Indeed, $m_{24} = 4$ and $m_{34} = 3$.

Funaizhang
  • 171