Why does the sign of this determinant change when changing the sense of vertices?

Question

The formula for finding the area of a triangle $ABC$ with vertices $A$ $(x_1,y_1)$, $B$ $(x_2,y_2)$, and $C$ $(x_3,y_3)$ is given by the following formula:

$$\Delta ABC = \frac 1 2\left|{\begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \end{array} } \right|$$

While the magnitude of the RHS gives the area. I don't really understand why the sign of the expression on the RHS changes when we change the rotational sense of the vertices A,B and C. (My book insists to take the vertices in clockwise sense) For example, when we take A,B and C in the clockwise sense, and if the expression turns to be positive, then if we take the vertices A,B and C in the counter-clockwise sense, then its expression is necessarily negative. Why is there a change of sign when we change the sense of rotation about the vertices A,B and C? Further, please explain why the expression is necessarily positive if the vertices are taken in clockwise sense and is negative if vertices are taken in anticlockwise sense.

Answer 1

Further, please explain why the expression is necessarily positive if the vertices are taken in clockwise sense and is negative if vertices are taken in anticlockwise sense.

Let's reduce the problem slightly - you can use the first point as the origin instead. Geometrically, this is a translation of all the points by a constant vector, and obviously doesn't affect the area. In terms of the determinant, this is achieved by applying the two column operations $$ C_1 \to C_1 - x_1C_3, \\ C_2 \to C_2 - y_1C_3, \\ $$ which do not change the determinant. So without loss of generality we may assume $\binom{x_1}{y_1} = \binom{0}{0}$, and now we need to check $$\frac 1 2\left|{\begin{array}{ccc} 0 & 0 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \end{array} } \right| >0? $$ Expanding this determinant (e.g. Laplace expansion along the top row) we obtain $$ \frac 1 2\left|{\begin{array}{ccc} 0 & 0 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \end{array} } \right| = \frac 1 2\left|{\begin{array}{cc} x_2 & y_2 \\ x_3 & y_3 \\ \end{array} } \right| = \frac12 \binom{-y_2}{x_2}\cdot\binom{x_3}{y_3}$$

This is maybe easier to interpret if we first assume that we rotated the diagram until the second point lies on the positive part of the $x$ axis. i.e. $y_2=0, x_2 > 0$. Now the determinant is simply

$$ x_2y_3/2 $$ and this is positive iff $y_3$ is positive, which is true iff you took the points in the anticlockwise order - not the clockwise order, as your book said*.

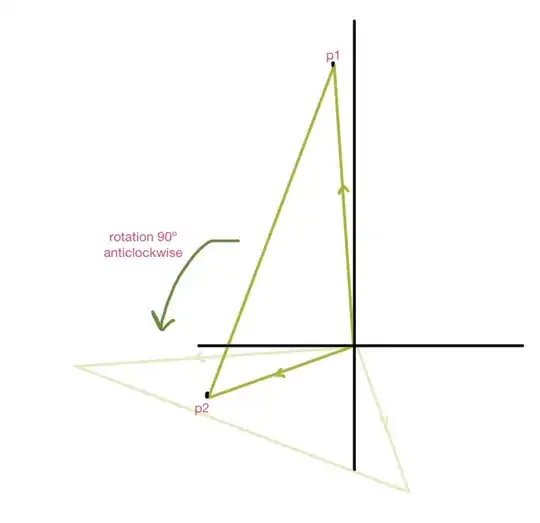
At this point, you can either wave your hands while saying something about rotation matrices having determinant 1, or you can repeat the argument for a general $\binom{x_2}{y_2}$. What does it mean to pick 3 points in counterclockwise order? It means that the third point is on the "left" side of the line joining the first two points. Since the first point is $\binom{0}{0}$, a vector parallel to this line is $\binom{x_2}{y_2}$, and the vector $$ \binom{-y_2}{x_2}$$ is the $90º$ anti-clockwise rotation of $\binom{x_2}{y_2}$. The third point $\binom{x_3}{y_3}$ is on the "left" side of the line iff the dot product of $\binom{x_3}{y_3}$ and $ \binom{-y_2}{x_2}$ is positive, whence the result. (in fact, I might take this as a definition of being on the "left" side...)

PS this is not very far from the full derivation of why this is equal to the area; For the full derivation, you may want to consult the answers here -

Show that the area of a triangle is given by this determinant

Proof the area of a given triangle with coordinates is half determinant

Why determinant of a 2 by 2 matrix is the area of a parallelogram?

---

*I checked to make sure with this explicit example: $ \tiny \begin{pmatrix} \scriptsize 0 & \scriptsize 0 &\scriptsize 1 \\\scriptsize 1 &\scriptsize 0 &\scriptsize 1 \\ \scriptsize 0 &\scriptsize 1 &\scriptsize 1 \end{pmatrix}$ has determinant 1, and the vertices $(0,0),(1,0),(0,1)$ are indeed taken in the anticlockwise sense. So either you copied something wrong or your book has a typo.

Answer 2

Changing the direction in which the vertices are taken permutes the rows of the $3×3$ matrix, and this is an odd permutation ($123$ becoming $132$ for example). Therefore, by the properties of determinants, the sign flips.

Answer 3

WLOG, $(x_1,y_1)=(0,0)$ and $(x_2,y_2)=(1,0)$ because you can translate the three points so that $P_1$ becomes the origin, then rotate so that $P_2$ comes on the $x$ axis and scale so that $\|P_1P_2\|=1$. None of these operations changes the sign of the determinant. (Rotation is expressed as a product with an orthogonal matrix, the determinant of which is $1$.)

Then

$$\begin{vmatrix}0&0&1\\1&0&1\\x_3&y_3&1\end{vmatrix}=y_3.$$

Hence the determinant is positive when the third point is to the left of the line from the first to the second.