8

I was recently reminded of this probability "paradox" (in quotes because in fact there's nothing really paradoxical about it, but it's surprising to the intuition), which I first encountered back in the rec.puzzles Usenet group. I want to know if it has a name. Here it is:

Suppose I write any two distinct (real) numbers on two blank cards that I then put face down. You get to look at the number on one of the cards, of your choice. Now, I ask you whether that number is the lower or the higher of the two. Can you answer in such a way that your probability of being correct is strictly greater than $\frac12$?

At first, it seems incredible that this is even being asked. I can use any method I choose to select the two numbers, and you have no way of knowing what the other number is. Nonetheless, you can answer in such a way that your response is more likely than not to be correct.

Method: Select any cumulative distribution function $F(x)$ that is strictly increasing; that is, pick a function $F(x)$ such that

  • $F(x) > F(y)$ for all $x > y$
  • $\lim_{x \to -\infty} F(x) = 0$
  • $\lim_{x \to +\infty} F(x) = 1$

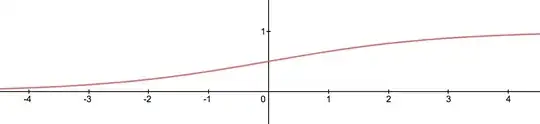
To make things simple, a suitable function is $F(x) = \frac{2^x}{1 + 2^x}$. (This is similar to the standard logistic function, but with base $2$ instead of base $e$.)

enter image description here

Now, if the number you look at is $x$, you say "higher" with probability $F(x)$, and "lower" with probability $1-F(x)$. For instance, if you turn over a card and see the number $3$, you say "higher" with probability $F(3) = \frac{2^3}{1+2^3} = \frac89$, and "lower" with probability $1 – F(3) = \frac19$.

Your probability of getting the right answer can now be determined as follows: Suppose the two numbers I selected were $a$ and $b$, with $b > a$. Your answer is correct if either you looked at $a$ and said "lower" (with probability $1-F(a)$), or you looked at $b$ and said "higher" (with probability $F(b)$). Since each of these two scenarios is equally likely—remember, you got to choose the card you looked at, with no prior information—your overall probability of guessing correctly is

$$ P(\text{correct}) = \frac{1-F(a)+F(b)}{2} = \frac12 + \frac{F(b)-F(a)}{2} $$

But since $F(x)$ is strictly increasing, and $b > a$, we must have $F(b) > F(a)$, and so your probability of being correct must be strictly greater than $\frac12$.

Has anyone else heard of this seeming paradox, along with a name?

Update (2019-10-16-0413Z): Math.SE didn't provide this tip before I posted the question, but now this shows up as a "related question": Who discovered this number-guessing paradox?

I'll have to take a closer look at that!

Brian Tung
  • 34,160
  • If you wrote "any two distinct" real numbers on two blank cards, then indeed you will not have a $1/2$ probability in almost no case. Your function in no case serve for that. For this to be a paradox, you should have an "almost zero" distribution everywhere, which will lead into a case where you can select any number with equal probability, AND also you will not be able to say if any number is greater or lower... – Brethlosze Oct 16 '19 at 02:13
  • I've certainly heard of this paradox multiple times -- once back at Berkeley in the 1980s, I think, and more recently during a course at Brown, probably 6 or 7 years ago. But I never heard it given a name, alas. It's certainly a fascinating observation that you can do (ever so slightly) better than $0.5$. :) – John Hughes Oct 16 '19 at 02:16
  • @Brethlosze: It's actually immaterial that it's a CDF (other than that it must satisfy the stated conditions). It's just a concise way of saying what kind of function $F(x)$ is; no distribution is ever actually referred to. It is possible, though, that the paradox can be interpreted in terms of the implied distribution, but I've never thought about that. – Brian Tung Oct 16 '19 at 02:46
  • @JohnHughes: Indeed! I should point out (you no doubt know) that the average gain* over $1/2$ is actually $0$, in the same way that the average value of the harmonic sequence is $0$, even though all its values are positive. (*For a suitable definition of average. ) – Brian Tung Oct 16 '19 at 02:48
  • The aparent paradox is representing the fact "choose any number" as a CDF. We know it should be uniform in $\mathbb R$, and also we know no CDF do that... – Brethlosze Oct 16 '19 at 03:00
  • @Brethlosze: No. We are not assuming any distribution that the numbers are chosen from. It could be any distribution at all; they could be independent or dependent. They could have been chosen from my birthday or my cousin-in-law's most recent lottery numbers. They merely have to be distinct. – Brian Tung Oct 16 '19 at 03:18
  • 2
    I don't know a name for the paradox-like-substance, but I've encountered a simple deterministic version of it: just pick some arbitrary cutoff (say, 7), and have your rule be that you'll say "higher" if the the number you see exceeds 7 and lower if it doesn't. If both numbers exceed 7, or if both are below 7, this gives you a 50/50 shot of winning. But if the two numbers straddle 7, then you're guaranteed to win. – Aaron Montgomery Oct 16 '19 at 03:57
  • @AaronMontgomery: Right. That's where $F(x)$ is the Heaviside step at (say) $x = 7$. I can't decide if this makes the so-called paradox more or less transparent. :-). I'm just surprised this doesn't have a name attached to it. – Brian Tung Oct 16 '19 at 04:02
  • It does look like a duplicate of the previous question. Vote to close? –  Oct 16 '19 at 04:47
  • A vague reference to a close one is referred to as the "Information Paradox" in here: https://courses.csail.mit.edu/6.042/past-devel/archive/spring94/misc/problems-ravi/probability.tex – NoChance Oct 16 '19 at 05:04
  • @Rahul: Possibly, but I'm inclined not to, since I didn't see a definitive name attached there. I'll have to take a closer look. (Of course, you're not beholden to my wishes here!) – Brian Tung Oct 16 '19 at 05:24
  • The question is a variant of the two envelopes problem - that often has one envelope having double the positive number of the other, but is not essential to its question, and in the original form does not involve inspecting the contents of one of the envelopes – Henry Oct 03 '22 at 07:55
  • @Henry: Interesting. I think of these two "two envelopes problems" as being distinctly different. – Brian Tung Oct 03 '22 at 07:58
  • @BrianTung - it is different, but I would suggest they are looking at something in different ways. In particular, if you can look at the contents of an envelope, then the strategy here starts to address the apparent paradox that at first sight changing envelopes and then changing again raises the expectation – Henry Oct 03 '22 at 09:52
  • @Henry: I think I see what you're saying, but I consider that to be a view from too high an altitude to consider them essentially just variations on a theme. At any rate, I think it warrants a different name. Maybe we'll have to agree to disagree. – Brian Tung Oct 03 '22 at 15:35

0 Answers0