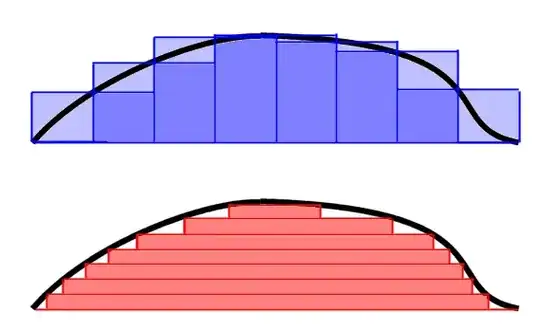
I was reading this beautiful discussion about the difference between Riemann and Lebesgue's integral .
What is not clear to me is the following: if we are computing the area we are computing the portion of the graph of $y=f(x)$ that lies between the horizontal lines $y=y_i$ and $y=y_{i+1}$, why do we approximate it by using $ \sum_{i=0}^{n-1} \mu(E_i)y_i^*$? Should not it be $\sum_{i=1}^{n} \mu(E_i)(y_i- y_{i-1})$, where $y_i- y_{i-1}$ would be the "height" and the measure $\mu(E_i)$ , assuming the domain of $f$ is $R$, would be the "length"?
Edit:
For instance, suppose I am approximating the area under the curve in figure 2 below through the red rectangles. Why do not we use simply $\sum_{i=1}^{n} \mu(E_i)(y_i- y_{i-1})$? For instance, the area of the rectangle on top, should be simply $\mu(E_n)(y_n- y_{n-1})$. Where $\mu(E_n)$ is $(x:y_{n-1}<f(x)<y_n)$. What is wrong with my reasoning?