Compute $\sum_{n=1}^\infty\frac{H_{n}^2}{(2n+1)^3}$

Question

How to prove

$$\sum_{n=1}^\infty\frac{H_{n}^2}{(2n+1)^3}=\frac{31}{8}\zeta(5)-\frac{45}{8}\ln2\zeta(4)+\frac72\ln^22\zeta(3)-\frac78\zeta(2)\zeta(3)$$

where $H_n$ is the harmonic number and $\zeta$ is the Riemann zeta function.

---

Here is my approach and would like to see different methods if possible.

Using the identity

$$\frac{\ln^2(1-x)}{1-x}=\sum_{n=1}^\infty (H_n^2-H_n^{(2)})x^n$$

replace $x$ with $x^2$, then multiply both sides by $\frac12\ln^2x$ and integrate from $x=0$ to $1$ we get

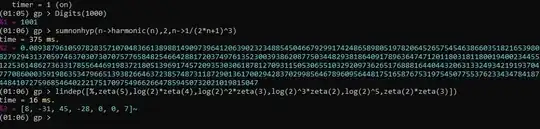
$$\sum_{n=1}^\infty\frac{H_n^2-H_n^{(2)}}{(2n+1)^3}=\frac12\int_0^1\frac{\ln^2x\ln^2(1-x^2)}{1-x^2}\ dx\\=\frac1{16}\int_0^1\frac{\ln^2x\ln^2(1-x)}{\sqrt{x}(1-x)}\ dx=\frac1{16}\left.\frac{\partial^4}{\partial a^2\partial b^2}\text{B}(a,b)\right|_{a\mapsto 1/2\\b\mapsto0^{+}}$$

with help of Mathematica we have

$$\left.\frac{\partial^4}{\partial a^2\partial b^2}\text{B}(a,b)\right|_{a\mapsto 1/2\\b\mapsto0^{+}}=248\zeta(5)-90\ln2\zeta(4)+56\ln^22\zeta(3)-112\zeta(2)\zeta(3)$$

Also, from here we have

$$\sum_{n=1}^\infty\frac{H_{n}^{(2)}}{(2n+1)^3}=\frac{49}{8}\zeta(2)\zeta(3)-\frac{93}{8}\zeta(5)$$

Combining these two result, we get the desired answer.

---

Note: You can find here details about the derivative of beta function.

Answer 1

Assuming that we know the value of ${\displaystyle \sum_{n\geq1}\frac{H_{n}^{\left(2\right)}}{\left(2n+1\right)^{3}}}$, we can use a classic result of Flajolet and Salvy:

Theorem. Assume that $r\left(s\right)$ is a rational function such that:

a) $r\left(s\right)=O\left(s^{-2}\right)$ at infinity,

b) $r\left(s\right)$ has no pole in $\mathbb{Z}\setminus\left\{ 0\right\}$.

Then $$2\sum_{n\geq1}r\left(n\right)H_{n}+\sum_{n\geq1}r^{\prime}\left(n\right)=-\sum_{\beta\in S}\underset{s=\beta}{\mathrm{Res}}\left(r\left(s\right)\left(\psi\left(-s\right)+\gamma\right)^{2}\right)$$ and $$3\sum_{n\geq1}r\left(n\right)H_{n}^{2}-3\sum_{n\geq1}r\left(n\right)H_{n}^{\left(2\right)}+3\sum_{n\geq1}r^{\prime}\left(n\right)H_{n}+\sum_{n\geq1}\left(\frac{r^{\prime\prime}\left(n\right)}{2}-3r\left(n\right)\zeta\left(2\right)\right)$$ $$=-\sum_{\beta\in S}\underset{s=\beta}{\mathrm{Res}}\left(r\left(s\right)\left(\psi\left(-s\right)+\gamma\right)^{3}\right)$$where $\psi\left(s\right)$ is the Digamma function and $S$ is the set of the poles of $r\left(s\right)$.

Then, tacking $r\left(s\right)=\left(2s+1\right)^{-3}$, we have $$3\sum_{n\geq1}\frac{H_{n}^{2}}{\left(2n+1\right)^{3}}-3\sum_{n\geq1}\frac{H_{n}^{\left(2\right)}}{\left(2n+1\right)^{3}}-18\sum_{n\geq1}\frac{H_{n}}{\left(2n+1\right)^{4}}$$ $$+\sum_{n\geq1}\left(\frac{24}{\left(2n+1\right)^{5}}-\frac{3\zeta\left(2\right)}{\left(2n+1\right)^{3}}\right)=-\underset{s=-1/2}{\mathrm{Res}}\left(\frac{\left(\psi\left(-s\right)+\gamma\right)^{3}}{\left(2s+1\right)^{3}}\right)$$ and, with $r(s)=(2s+1)^{-4},$ $$2\sum_{n\geq1}\frac{H_{n}}{\left(2n+1\right)^{4}}-8\sum_{n\geq1}\frac{1}{\left(2n+1\right)^{5}}=-\underset{s=-1/2}{\mathrm{Res}}\left(\frac{\left(\psi\left(-s\right)+\gamma\right)^{2}}{\left(2s+1\right)^{4}}\right).$$ Combining these results, we get the thesis.

Answer 2

Considering that Euler-Zagier Sum has weight 2 + 3 = 5, result is a linear combination of $log(2)^k\zeta(m)\zeta(n)$ such that $k,m,n$ are non-negative integers (factor is omitted if any of them is 0) and $k+m+n=5$, (note that log(2) plays the role of "$\zeta(1)$"), we use Pari/GP v2.14 to get the following output

and voilá.