1

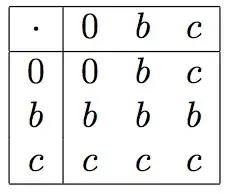
Associative law, in mathematics, either of two laws relating to number operations of addition and multiplication, stated symbolically: a + (b + c) = (a + b) + c, and a(bc) = (ab)c; that is, the terms or factors may be associated in any way desired. Source: Brittanica

Following this description, the usual example used to describe this law is: \begin{equation} \ a+(b+c)=(a+b)+c \end{equation} or \begin{equation} \ a(bc)=(ab)c \end{equation}

Since the description (I don't know whether it is valid enough) states that the terms may be associated in any way desired, isn't it also valid to do this in one step without making use of commutative law: \begin{equation} \ a+(b+c)=(a+c)+b \end{equation} \begin{equation} \ a(bc)=(ac)b \end{equation} Because I think this a + (b + c) has two units, of which a unit also consists of two units. Since associative law states that a child unit can be transferred to another parent unit. Why not transfer c directly to first unit without making use of a + b = b + a.

P.S. I am not very educated in mathematics or logic. Forgive my incorrect tagging. I only seek the explanation of why this doesn't work.

Yanek Yuk
  • 11
  • 1
    There is from one point of view an interesting (to mathematicians) and deep question here, but the answer to that will unfortunately not be one that is helpful for you. I think the question probably needs a more elementary answer (and that is no disrespect meant; but this is a site for research mathematicians, so we see things differently, even when they seem simple). I have voted to move to math.stackexchange – theHigherGeometer Sep 26 '19 at 12:16
  • No offense was taken. You're right. I didn't know about math.stackexchange. Is there any way that I can just move this question, or should I wait for it to happen? –  Sep 26 '19 at 12:19
  • 1
    @DavidRoberts I'm curious what you have in mind. Care to give a hint? – Alex Kruckman Sep 26 '19 at 13:28
  • 2
    As far as I can see, this is just a problem of semantics. Here, “associated in any way desired” means that in an unbracketed expression like $x_1+x_2+\dots+x_n$, we may insert brackets in an arbitrary way such that the result is a well-formed expression using binary $+$, and we always get the same result. This does not include the transformation made in the OP. – Emil Jeřábek Sep 26 '19 at 13:51
  • I agree with Emil's assessment. The OP seems to misinterpret the phrase "associate in any way desired". Someone should explain this intuitively in an answer. There are formal proofs in the MSE thread How does one actually show from associativity that one can drop parentheses? – Bill Dubuque Sep 26 '19 at 14:50
  • @AlexKruckman there's an ongoing discussion starting here about cartesian monads and symmetric vs non-symmetric operads that is relevant to the equations suggested by the OP – theHigherGeometer Sep 26 '19 at 21:13
  • @Yanek well, it just happened, so there you go :-) – theHigherGeometer Sep 26 '19 at 21:14

1 Answers1

2

If it was so, then having a $0$ element in $(A,+)$, from associativity we would get commutativity, like this: $$x + y = (0 + x) + y = 0 + (y + x) = y + x.$$ This is not the case, as the example in the following table shows:

enter image description here

(Read the operation symbol as $+$.) Here, $b+c = b \neq c = c+b$.
It is easy to check that the associativity law is satisfied.

amrsa
  • 12,917
  • 2
    Simpler to use the free monoid on $a,b,c$, i.e. all strings with those letters and concatenation as the operation. – Bill Dubuque Sep 26 '19 at 14:48
  • @BillDubuque Indeed, and that example didn't even occur to me. Still, it might be useful for some users who might be more comfortable with a finite example... – amrsa Sep 26 '19 at 15:33
  • Yes, I had to replace all the 0 with a to understand it clearly. Apart from that, what I understand is that I have to think of associativity exclusively separate from commutativity. Because, otherwise, in my perspective, the example operation you've provided is simply "not associative" rather than "associative but not commutative." – Yanek Yuk Sep 26 '19 at 16:41
  • @YanekYuk Yes, this example shows that associativity doesn't entail commutativity; the converse also applies (examples can be founded), and so these are independent. About the $0$ element, the idea was to facilitate, since it is neutral, but it seems like you understood it anyway. Do you think this answer cleared your doubts? – amrsa Sep 26 '19 at 17:52