I've always heard this reasoning, and it makes obvious sense, but how do you actually show it for some arbitrary product? Would it be something like this?
$$(a(b(cd)))e=((ab)(cd))e=(((ab)c)d)e=abcde?$$
Do you just say that the grouping of the parentheses now corresponds to just multiplying straight through? Thanks.
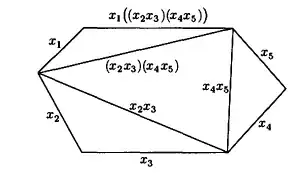
You can prove by induction on the number of factors that all such products are equal. We show that if you have $a_1,\ldots,a_n$, then any way to place the parenthesis will yield the same result as $a_1(a_2(\cdots(a_{n-1}a_n)\cdots))$.
If the number of factors is $1$ or $2$, then the result is immediate. If the number of factors is $3$, then it follows precisely by associativity: $(a_1a_2)a_3 = a_1(a_2a_3)$.
Assume the result holds for any $k$, $1\leq k\lt n$, and you have some product of $n$ elements $a_1,\ldots,a_n$, in order, with parentheses placed in some arbitrary (but valid) manner. Then there exists $k$, $1\leq k\lt n$, such that the product is of the form $$w_1(a_1,\ldots,a_k)\cdot w_2(a_{k+1},\ldots,a_n)$$ where $w_1(a_1,\ldots,a_k)$ is just an expression involving the product of $a_1,\ldots,a_k$ with parentheses placed in some fashion, and similarly with $w_2$. (We are just looking at the "last" product to be done; e.g., if you have $((a_1a_2)a_3)(a_4a_5)$, we would have $k=3$, $w_1(a_1,a_2,a_3) = (a_1a_2)a_3$, and $w_2(a_4,a_5) = a_4a_5$; if you have $a_1((a_2a_3)(a_4a_5))$, then $k=1$, $w_1(a_1) = a_1$, and $w_2(a_2,a_3,a_4,a_5) = (a_2a_3)(a_4a_5)$; etc).
By induction we can write $$w_1(a_1,\ldots,a_k) = a_1(a_2(\cdots(a_{k-1}a_k)\cdots))$$ so \begin{align*} w_1(a_1,\ldots,a_k)w_2(a_{k+1},\ldots,a_n) &= \Bigl(a_1\bigl(a_2(\cdots(a_{k-1}a_k)\cdots)\Bigr)\cdot w_2(a_{k+1},\ldots,a_n)\\\ &= a_1\cdot\Bigl(a_2(\cdots(a_{k-1}a_k)\cdots)w_2(a_{k+1},\ldots,a_n)\Bigr) \\\ &= a_1\cdot\Bigl( a_2(a_3(\cdots(a_{n-1}a_n)\cdots)\Bigr) \end{align*} where the last equality follows from the induction hypothesis applied to a product with $n-1$ factors, and the immediately preceding equality by simple associativity of three factors, applied to $a_1$, $a_2(\cdots(a_{k-1}a_k)\cdots)$, and $w_2(a_{k+1},\ldots,a_n)$. (Note: If $k=1$, then you can skip directly from the first line to the last line without having to invoke associativity; the argument still holds.)
Thus, any expression of a product of $a_1,\ldots,a_n$, in that order, with parentheses placed in an arbitrary but valid manner, is equal to $$a_1(a_2(\cdots(a_{n-1}a_n)\cdots)),$$ This completes the induction and the proof.
Since all ways of associating a product of $n$ factors, $a_1,\ldots,a_n$ yield results that are equal to one another, we may freely write any such product simply as $a_1\cdots a_n$ to represent their common value.
Hint $ $ It's easy: iteratively push ')'s rightward via the rewrite rule $\rm\, (xy)z\ \to\ x(yz).\,$ This process terminates with the right-associated normal form where all ')'s are at the right end, namely $\rm\ a(b(c(d(\cdots))),\, $ written $\rm\ abc\cdots $ (unambiguous - since every bracketing rewrites to it by below).
Proof $ $ (sketch) $ $ by strong induction on the length $\rm\:\ell(Z) = $ number of operands (factors)
$\rm \ell(Z)\, =\, 1\!:\ \ \ Z = a\ $ is in normal form $ $ (base case).
$\rm \ell(Z)\, >\, 1\!:\ \ \ Z = XY\ $ where $\rm\:\ell(X),\ell(Y)< \ell(Z)\,$ splits into $2$ cases:
$\rm\ \ \color{#90f}{\ell(X)\! =\! 1}\!:\ \ \ XY = a\color{#c00}Y = a(\color{#c00}{b(c(\cdots))})\:\ $ by $\:\rm\color{#90f}{X= a},\,$ and $\rm\color{#c00}{induction}$ applied to $\rm\color{#c00} Y$
$\rm\ \ \ell(X)\! >\! 1\!:\ \ \ \color{#c00}XY = \underbrace{(\color{#c00}{a \bar X})Y = a(\color{#0a0}{\bar X Y})}_{\rm \color{darkorange}{associative}\ law} = a(\color{#0a0}{b(c(\cdots))})\ $ by $\rm\color{#c00}{induc}\color{#0a0}{tion}$ applied to $\rm \color{#c00}X,\, $ then $\rm\color{#0a0}{\bar XY}$
Only $\rm\color{darkorange}{associativity}$ $\rm\, (AB)C = A(BC)\,$ was used, so the proof works for any associative operation.
That «one can drop the parentheses» really means that «no matter how you put the parentheses in, the result will be the same».
To prove such a statement, what one usually does is pick one specific way of putting in parentheses, and shows that any other way gives the same result as the one we picked. This is done by induction in the number of factors.
Some enterprising soul might post a complete proof...
We argue by induction on the number $n$ of factors, assuming, as we may, $n\ge4$.
By induction hypothesis, we know that, for $k < n$, any product of the factors $b_1,\dots,b_k$ taken in this order can be written unambiguously as $b_1\cdots b_k$.
Then a product of any given sequence $a_1,\dots,a_n$ is necessarily of the form $$ c_k:=(a_1\cdots a_k)(a_{k+1}\cdots a_n) $$ for some $k=2,\dots,n-1$, and we only need to check $$ c_p=c_q\quad\forall\quad1 < p < q < n, $$ which we do as follows: $$ \begin{matrix} &(a_1\cdots a_p)&(a_{p+1}\cdots a_q& a_{q+1}\cdots a_n)\\ \\ =&(a_1\cdots a_p)&((a_{p+1}\cdots a_q)&(a_{q+1}\cdots a_n))\\ \\ =&((a_1\cdots a_p)&(a_{p+1}\cdots a_q))&(a_{q+1}\cdots a_n)\\ \\ =&(a_1\cdots a_p&a_{p+1}\cdots a_q)&(a_{q+1}\cdots a_n). \end{matrix} $$
Here is a geometric version of a proof:
First, note that parenthecizings of a product of length n are in bijection with triangulations of convex (n+1)-gon $A$. This is illustrated in the picture below, copied from p. 240 of the book “Discriminants, Resultants, and Multidimensional Determinants” of Gelfand Kapranov and Zelvinski.
In words, to go from triangulations of $A$ to parenthecizings of $x_1x_2\ldots x_n$, label all but one edges of $A$ in order as $x_1, x_2, \ldots, x_n$, leaving the last edge as “output edge”. Then a triangulation of $A$ gives a parenthesizing in an inductive manner: Take the triangle $T$ incident on the output edge; then $A$ with $T$ removed is a union of two polygons $A_l$ and $A_r$ (one of which could be degenerate, i.e. a segment), each of which is incidents on one “non-output” edge of $T$. Then assign to our triangulations the product of parenthecizings assigned to $A_l$ and $A_r$.
One can easily go back in a similarly inductive manner, by thinking of a parentecising $p$ as a product of two subparenthesizings $p_l$ and $p_r$, and correspondingly getting the triangulation associated to $p$ by “inserting a triangle $T$” into the triangulations of smaller polygons associated to these $p_l$ and $p_r$.
Now that we have a geometric interpretation of parenthecizings, we can give geometric interpretation of single application of associativity law. This is known as a flip — in a given triangulation, one takes two triangles sharing an edge, thus forming a quadrilateral, and replaces this edge with the other diagonal of this quadrilateral.
Thus the question becomes: can we connect any two triangulations of a convex polygon by a sequence of “diagonal flips”? The answer is yes, and again is best illustrated by a picture, this time stolen from page 7 of book “Triangulations” by Jesús A. De Loera, Jörg Rambau, and Francisco Santos.
In words, pick any vertex $i$ and make triangulation by drawing all diagonal from that vertex. To connect any triangulation to that “i-standard” one, make flips that increase the degree of $i$: as long as you are not at “i-standard” triangulation, there exists a triangle $T$ with vertex $i$ and opposite edge not an edge of $A$ (but rather a diagonal); complete $T$ to a guadrilateral, and flip the diagonal.
This shows that “the graph of flips of the triangulations of the n-gon” is connected (thus establishing what we want).
QED!
In fact much more is true. The graph of flips is just the union of 1 dimensional faces of a convex polytope, all of whose faces correspond to incomplete triangulations/incomplete parenthecisings, the one open face corresponding to incomplete triangulation with no triangles/incomplete parenthecising with no parenthesis. What we proved is simply that one can get from any vertex of this polytope to any vertex by following some edges. This is of course true for any convex polytope (take the straight path and push it to faces of lower and lower dimension, for example by projecting "radially" from a point of the face not on the path; this is an easy version of cellular approximation theorem in algebraic topology).
The polytope in question is called an associahedron, or Stasheff polytope, and its existence follows from various direct constructions, notably it is constructed by Gelfand-Kapranov-Zelevinsky as the secondary polytope of a convex n-gone in the plane (this is described in the same book where the first picture came from).
On a related and more ridiculous note, existence of a permutohedron (secondary polytope of the prism $I\times \Delta^n$ on the simplex $\Delta^n$) shows that commutativity law allows one to write products of any number of elements in any order (this is equivalent to showing that the permutation group is generated by transpositions).
A more formal pedantic version of part a very small part of Mariano Suárez-Alvarez' answer.
Associativity is a property of multiplication, which is a binary operation. More precisely, multiplication is a map $m:R \times R \to R, (a,b) \mapsto m(a,b)=ab$.
The associative law says that (ab)c = a(bc). Using m, that is the same as m(m(a,b),c) = m(a,m(b,c)). (Note that m takes exactly two elements of $R$ as "input"). A consequence of the associative law is that there is no ambiguity in writing abc, since «no matter how you put the parentheses in, the result will be the same».
Edit:As Arturo writes in a comment below: "associativity is not a property of multiplication per se ([...] addition [is] associative [as is] composition of functions) but rather, a property that a binary operation may or may not have." Of course, Arturo's proof in his answer works for any associative binary operation.