$x \cos \theta - y \sin \theta = \cos 2\theta$
$x \sin \theta + y \cos \theta = 2 \sin 2\theta$
I tried to use cross multiplication method to find $\cos \theta$ and $\sin \theta$ and then put the values in $\cos^2 \theta + \sin^2 \theta = 1$, but was not able to eliminate $\cos 2\theta$ or $\sin 2\theta$. Please help me in solving this question.
Multplying the first equation by $\sin \theta$ gives
$$x \cos\theta\sin \theta -y\sin^2\theta = \sin\theta \cos 2\theta\tag{1}$$
and the second by $\cos \theta$ will give
$$ x \cos\theta\sin \theta + y \cos^2\theta = 2\sin 2\theta \cos \theta\tag{2}$$
so we can eliminate the $x$ by subtracting 1 from 2:
$$y (\cos^2 \theta + \sin^2 \theta) = 2\sin 2\theta \cos \theta - \sin\theta \cos 2\theta$$
so $$y = 2\sin 2\theta \cos \theta - \sin\theta \cos 2\theta$$
Now we can maybe simplify by using the double angle formulae:
$$\sin 2\theta = 2\sin \theta \cos \theta$$ and
$$\cos 2\theta = \cos^2 \theta - \sin^2 \theta$$
Try it. And then solve $x$ by a similar multiplication and substraction or adding.
Once solved in $\theta$ you'll get $\begin{cases} x &= &3\cos(\theta)-2\cos(\theta)^3 \\ y &= &3\sin(\theta)-2\sin(\theta)^3 \end{cases}$
https://www.desmos.com/calculator/xdlons0rzq
You can graph it (green curve) and notice this is an astroid.
Although it is rotated and stretched compared to the reference astroid (the one inscribed in the unit circle: wikipedia:astroïde)
So we will first apply the transformation $\begin{cases} u=\frac{x+y}{2\sqrt{2}}\\v=\frac{x-y}{2\sqrt{2}}\end{cases}$
To obtain the red curve which is now the standard one.
According to the wiki page it has equation $$(u^2+v^2-1)^3+27u^2v^2=0$$
Bu substituting $x,y$ we can get a cartesian equation but it is not very nice:
$x^6+3x^4y^2+3x^2y^4+y^6+15x^4-78x^2y^2+15y^4+48x^2+48y^2-64=0$
$$x \cos (\theta)-y \sin (\theta)=\cos (2 \theta )\tag 1$$ $$x \sin (\theta)+y \cos (\theta)=2\sin (2 \theta )\tag 2$$
$$(1)^2+(2)^2\implies x^2+y^2=4 \sin ^2(2 \theta)+\cos ^2(2 \theta)=\frac{1}{2} (5-3 \cos (4 \theta))\implies \theta=??? $$
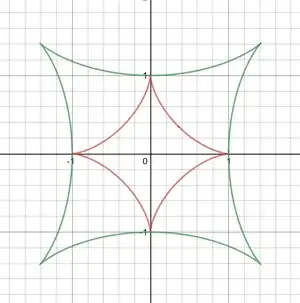
Continued on with @Henno_Brandsma y expression, and let $s=\sin\theta, c=\cos\theta$:
$y = 2\sin 2\theta \cos \theta - \sin\theta \cos 2\theta = 4s(1-s^2)-s(1-2s^2) = 3s-2s^3$
Substitute back to equation 1:
$cx = \cos(2\theta) + s(3s-2s^3) = (2c^2-1)+(1-c^2)(1+2c^2)=3c^2-2c^4$
$$x = 3c-2c^3$$
We want even powers for s and c, so that we can use identity, $s^2 + c^2 = 1$
$x^2 = (3c-2c^3)^2 = \large 2 - {3(2c^2-1)^2 \over 2} + {(2c^2-1)^3\over2}=2-{3\cos^2(2\theta)\over 2}+{\cos^3(2\theta) \over2}$
$y^2 = (3s-2s^3)^2 = \large 2 - {3(2s^2-1)^2 \over 2} + {(2s^2-1)^3\over2}=2-{3\cos^2(2\theta)\over 2}-{\cos^3(2\theta) \over2}$
$$x^2-y^2 = \cos^3(2\theta)$$ $$x^2+y^2 = 4-3\cos^2(2\theta)$$
$$\cos^6(2\theta)=(x^2-y^2)^2=\left({4-x^2-y^2 \over 3}\right)^3$$ $$y^6+(3x^2+15)y^4 + (3x^4-78x^2+48)y^2+(x^6+15x^4+48x^2-64)=0$$
Square and add to find $$x^2+y^2=\cos^22t+4\sin^22t$$
$$2(x^2+y^2)=1+\cos4t+4(1-\cos4t)$$
$$\implies\cos4t=?$$
To eliminate $2t,$
$$(2\cos2t)^2+(2\sin2t)^2=x^2(\sin^2t+(2\cos t)^2)+y^2(4\sin^2t+\cos^2t)$$
$$\implies8=x^2(1-\cos2t+2(1+\cos2t))+y^2(2(1-\cos2t)+1+\cos2t)$$
$$\implies\cos2t=?$$
Now use $\cos2(2t)=2(\cos2t)^2-1$ to eliminate $2t$
