The Context
The origin of my question is my own answer to this question, where the continuity of the function $f: [0,1) \to [0,1)$ that only preserves the odd digits of its input value is analyzed.
In this context, I will slightly modify the definition given there, as follows.
The function I am considering now is $f: [0,+\infty) \to [0,+\infty)$ that preserves only the even digits of the input. So if $x$ has decimal expansion
$$x = \sum_{k=-\infty}^{+\infty}a_k 10^k,$$
then
$$f(x)=\sum_{k=-\infty}^{+\infty}a_{2k}10^{k}.$$
So for example
$$f(5\textbf{8}7\textbf{4}1\textbf{2}.7\textbf{8}0\textbf{3}4\textbf{0}5\textbf{1})=842.8301.$$
With a very similar approach to the one given here, it can be shown that $f$ is continuous almost everywhere (the only exception being the numbers whose least significant digit occupies an odd position), and right-continuous everywhere.
Edit. I am assuming, as in the original question, to adopt, in case of ambiguity, the finite version of the number's decimal expansion.
Note the self-similarity
$$f\left(10^{2k} x\right)=10^k f(x), \ \ \forall k\in \Bbb Z.$$
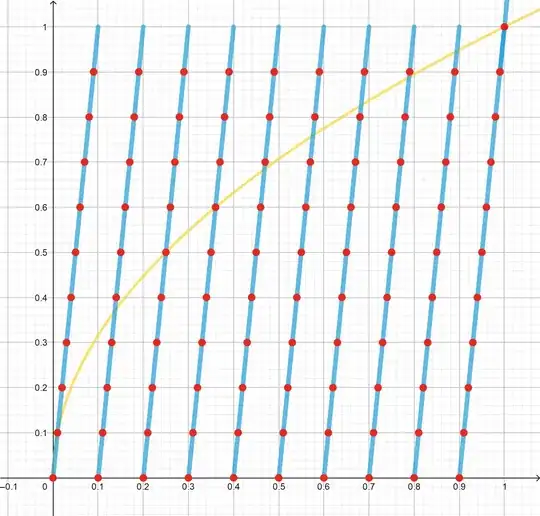
Below an approximate plot of the function $f$ in the range $[0,1]\times[0,1]$.
Red dots represent points actually belonging to the graph of $f$. The yellow line represents the graph of $$s(x) = \sqrt x.$$ By self-similarity, a scaling of $10^{2k}$ of the $x$-axis and of $10^{-k}$ of the $y$-axis, for any $k\in \Bbb Z$, would give an exact replica of the given plot.
Introductory Observation
Aside from the trivial intersections between $f$ and $s$, that is all the points with coordinates
$$\left(10^{2k},10^k\right),$$
there are many other interesting intersections, such as (limiting ourselves to the range shown in the picture)
$$(0.25,0.5),$$ $$(0.36,0.6),$$ $$(0.0121,0.11),$$ and 'trikiest' ones, such as $$(0.5776,0.76),$$ or even $$(0.35295481,0.5941).$$
The Question
Is there any non-terminating decimal (or even irrational) $x$ such that $$y=f(x) = s(x),$$ that is, is there any non-terminating decimal $y$ whose square contains - in the even positioned digits - the digits of the original number $y$?
Edit. I emphasize again that no infinite sequences of $9$'s are allowed, since we are adopting the finite decimal expansion version of the number, if this ambuiguity arises.