Continuity in $0$
To show continuity in $0$, take any sequence $(a_n)$ converging to $0$, with $0< a_n < 1$. Convergence of $(a_n)$ implies that for any given $k\in \Bbb Z^+$, and for sufficiently large $n$,
$$a_n \leq 10^{-2k}.$$
As a consequence,
$$f(a_n) \leq 10^{-k}.$$
So, by taking $n$ large enough, $f(a_n)$ can be made arbitrarily small and thus the squence $(f(a_n))$ converges to $f(0) = 0$.
Example point where the function is not continuous
Take now, for example, $x_0 = 10^{-2m}$, with $m\in \Bbb Z^+$, so that
$$f(x_0) = 0.$$
The sequence
$$a_n = \sum_{k=1}^n 9\cdot 10^{-2m-k}, \ \ \ n\in \Bbb Z^+,$$
converges to $x_0$. However
$$f(a_n) = \sum_{k=1}^{\left\lfloor\frac{n-1}2 \right\rfloor}9\cdot 10^{-m-k}$$
converges to $10^{-m} \neq f(x_0)$, making the function not continuous in $x_0$.
Further discussion on continuity
It is straightforward to extend the above path to any $x_0\neq 0$ with finite decimal representation where the least significant digit occupies an even position. In all these points the function is not continuous. See Edit 1 at bottom.
On the other hand, if $x_0$ has finite decimal representation and the least significant digit occupies an odd position, then the function is continuous in $x_0$. See Edit 2.
If $x_0$ has infinite decimal representation, then $f$ is continuous in $x_0$. See Edit 3.
So the function is not continuous only on a subset of $\Bbb Q$, which makes it a Riemann-integrable function.
Further discussion on differentiability
The function $f$ is nowhere differentiable. In fact the limit of the difference quotient
$$\lim_{x\to x_0} q_{x_0}(x) = \lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}$$
never converges. However it does exist (and it is equal to $+\infty$) almost everyhere, that is at all points having infinite decimal representation. See Edit 4 for details.
How the function graph looks like
In the first figure below you see an approximate plot of $f(x)$, the red dots representing some of the points that belong to the grah of $f$. The function is constrained within the light blue regions.
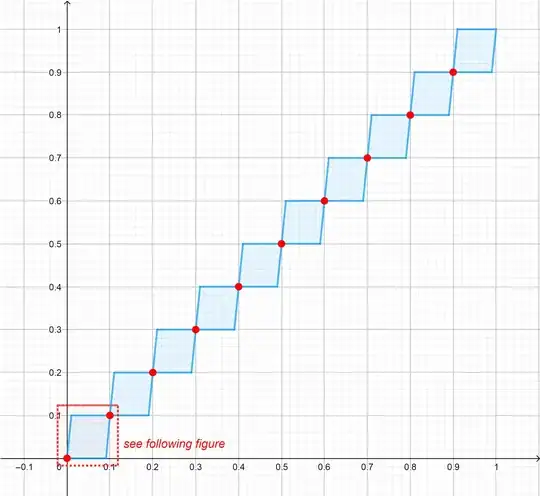
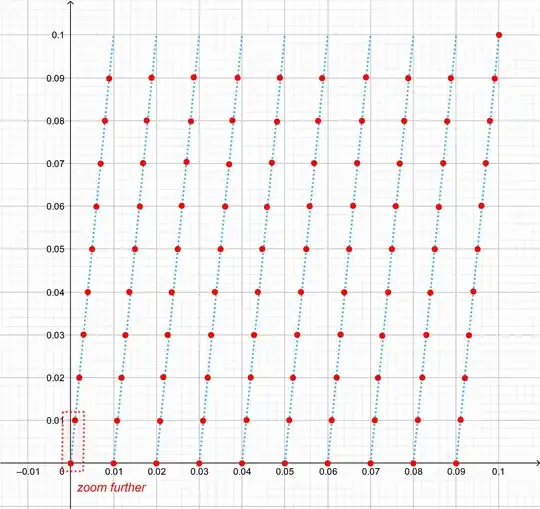
These regions can be obtained by shifting the first one of them, which is plotted, after magnification of a factor $10$, in the following figure. Again red dots are points belonging to the graph of $f$. A further zoom by a factor $100$, and a scaling of the $y$ axis, will give as result an identical copy of the graph given below. And so on for every interval of the form $x\in[0,10^{-2k+1}]$, $y\in [0,10^{-k}]$, $k\in\Bbb Z^+$.
Edit 1. Continuity - Finite decimal representation - least significant digit in even position
Let $x_0$ have decimal representation
$$ x_0= \sum_{k=1}^{2m}x_k\cdot 10^{-k}$$
for some $m \in \Bbb Z^+$, and $x_{2m}> 0$.
We have
$$f(x_0) = \sum_{k=1}^mx_{2k-1}\cdot 10^{-k}.$$
Consider the sequence
$$a_n = \sum_{k=1}^{2m-1}x_k\cdot 10^{-k}+ (x_{2m}-1)\cdot 10^{-2m}+\sum_{k=1}^n 9\cdot 10^{-2m-k}, \ \ \ n\in \Bbb Z^+.$$
Clearly $(a_n) \to x_0$. We also have
$$f(a_n) = f(x_0) + \sum_{k=1}^{\left\lfloor\frac{n-1}2 \right\rfloor}9\cdot 10^{-m-k}.$$
So $(f(a_n)) \to f(x_0) + 10^{-m}\neq f(x_0)$, and the function is therefore not continuous in $x_0$.
Edit 2. Continuity - Finite decimal representation - least significant digit in odd position
Let $x_0$ have decimal representation of the form
$$ x_0= \sum_{k=1}^{2m-1}x_k\cdot 10^{-k}$$
for some $m \in \Bbb Z^+$, and $x_{2m-1}> 0$.
Again we have
$$f(x_0) = \sum_{k=1}^mx_{2k-1}\cdot 10^{-k}.$$
Suppose the function is not continuous in $x_0$. Thus there must be a sequence $(a_n) \to x_0$ such that $(f(a_n))\not \to f(x_0)$. This in turn implies that, for any $N\in \Bbb Z^+$, there is $\epsilon$ such that
$$|f(a_n) - f(x_0)| \geq \epsilon,$$
for some $n>N$. Consider now $h \in \Bbb Z^+$ such that and $\epsilon > 10^{-m-h}$. So we either have
$$f(a_n) > f(x_0) + 10^{-m-h}\tag{2}\label{2}$$
or
\begin{eqnarray}f(a_n) < f(x_0) - 10^{-m-h}&=&f(x_0)- 10^{-m}+\sum_{k=1}^{h}9\cdot 10^{-m-k}.\tag{3}\label{3}\end{eqnarray}
If \eqref{2} occurs, then it must be
$$a_n > x_0 + 10^{-2m+1-2h}.\tag{4}\label{4}$$
If \eqref{3} occurs, then
$$a_n<x_0 - 10^{-2m+1} + \sum_{k=1}^{2h}10^{-2m-k}.\tag{5}\label{5}$$
Since either \eqref{4} or \eqref{5} occurs for some $n> N$, no matter how large we take $N$, $(a_n)$ does not converge to $x_0$, and we have a contradiction. Thus $f(x)$ is continuous in $x_0$.
Edit 3. Continuity - Infinite decimal representation.
Since, as required by OP, we adopt the finite decimal representation version of the number in case of infinite tail of $9$'s, any digit of $x_0$ (having infinite decimal representation) is at most followed by a finite sequence of $0$'s or $9$'s.
For any $\epsilon>0$, we aim at finding a $\delta(\epsilon)$, such that, for all $x$ satisfying
$$|x_0-x| < \delta(\epsilon),$$
we have
$$|f(x_0)-f(x)| < \epsilon.$$
Take $k$ so that
$$10^{-k}\leq \epsilon.$$
In order to obtain
$$f(x) < f(x_0) + 10^{-k}$$
we need the carry due to the addition not to affect the $k$th digit. If $t\geq 0$ is the number of consecutive $9$'s following the $k$th digit of $x_0$, then we must choose
$$x < x_0+10^{-2k-t+1}.$$
Similarly, in order to have
$$f(x) > f(x_0) - 10^{-k},$$
we can decrement the first non-null digit after the $k$th digit. So if $s\geq 0$ is the number of consecutive $0$'s following the $k$th digit of $x_0$ then we need
$$x > x_0 - 10^{-2k-s+1}.$$
Thus we can choose
$$\delta(\epsilon) = 10^{-2k-\max\{t,s\}+1}.$$
And this demonstrates the continuity of $f(x)$ in $x_0$.
Edit 4. Limit of the difference quotient
Let us first show that the limit
$$\lim_{x\to x_0}q_{x_0} (x)$$
does not exist if $x_0$ has finite decimal representation. At this aim, let $m\in\Bbb Z^+$ be the least significant digit of $x_0$, $o_n$ the null sequence
$$o_n = 10^{-2\left(\left\lfloor\frac m2\right\rfloor+n\right)+1}, \ \ n\in \Bbb Z^+$$
and $e_n$ the null sequence
$$e_n = 10^{-2\left(\left\lfloor\frac m2\right\rfloor+n\right)}.$$
The sequences
$$a_n = x_0+o_n$$
and
$$b_n = x_0+e_n$$
both converge to $x_0$. We have now
$$q_{x_0}(a_n) = \frac{f(a_n)-f(x_0)}{o_n} = \frac{10^{-n}}{o_n}=10^{n-2\left\lfloor\frac m2\right\rfloor},$$
so that $(q_{x_0}(a_n))\to+\infty$, and
$$q_{x_0}(b_n) = \frac{f(b_n)-f(x_0)}{e_n}=0,$$
so that $(q_{x_0}(b_n)) \to 0$. Therefore the limit does not exist.
Consider now a point $x_0$ with infinite decimal representation. We want to show, first, that
$$\lim_{x\to x_0^+}q_{x_0}(x) = +\infty.$$
Consider a null sequence $(d_n)$, with $0<d_n<1$, and let $k$ the first non-null digit of $d_n$, that is
$$k = -\left\lfloor\log_{10}d_n\right\rfloor.$$
Let also
$$a_n = x_0+d_n,$$
a sequence converging to $x_0$.
Now, the addition $x_0+d_n$ affects at least the $\lfloor\frac{k+1}2\rfloor$th digit of $f(x_0)$ (it may affect more significant digits because of the carry), so that
$$f(x)-f(x_0)\geq 10^{-\left\lfloor\frac{k+1}2\right\rfloor}\tag{6}\label{6}.$$
Condition \eqref{6} and the fact that $d_n < 10^{-k+1}$ yield
$$q_{x_0}(x) = \frac{f(x)-f(x_0)}{d_n}> \frac{10^{-\left\lfloor\frac{k+1}2\right\rfloor}}{10^{-k+1}}\geq 10^{-\frac k2}.$$
Therefore, by taking $n$ large enough, we can make the difference quotient $q_{x_0}(x)$ arbitrarily large. And thus the limit exists and it is $+\infty$.
A similar approach can be used to demonstrate that also
$$\lim_{x\to x_0^-}q_{x_0}(x) = +\infty.$$
A different approach (later edit)
Some insight can be obtained by considering that $f(x)$ can be written as
\begin{eqnarray}
f(x) &=& \sum_{n=1}^{+\infty} f_n(x)=\\
&=&\sum_{n=1}^{+\infty} \left[\frac{\left(10^{2n-1}x\right)}{10^{n-1}}-\frac{\left(10^{2n}x\right)}{10^{n}}\right]
\end{eqnarray}
where $(x)$ denotes the fractional part of $x$.
Note, for example, that the above series converges uniformly, by Weierstrass M-test. Then, since for all $n\in \Bbb Z^+$ $f_n(x)$ is continuous at all irrational points, so is $f(x)$. Uniform continuity and Riemann integrability of $f_n(x)$ guarantees also integrability of $f(x)$.

