how to find surface area of a sphere

Question

could any one tell me how to calculate surfaces area of a sphere using elementary mathematical knowledge? I am in Undergraduate second year doing calculus 2. I know its $4\pi r^2$ if the sphere is of radius $r$, I also want to know what is the area of unit square on a sphere.

Answer 1

You can even do it by using techniques from first-year calculus, and without using polar coordinates. Rotate the half-circle $y=\sqrt{r^2-x^2}$, from $x=-r$ to $x=r$, about the $x$-axis. Better, rotate the quarter circle, $0$ to $r$ about the $x$-axis, and then double the answer. So by the usual formula for the surface area of a solid of revolution. we want $$\int_0^r 2\pi x\sqrt{1+\left(\frac{dy}{dx}\right)^2}\,dx.$$

Find $\frac{dy}{dx}$. We get $-\frac{x}{\sqrt{r^2-x^2}}$. Square this, add $1$, bring to a common denominator, take the square root. So now we need $$\int_0^r 2\pi r\frac{x\,dx}{\sqrt{r^2-x^2}}.$$ The integration is straightforward. Either let $u=r^2-x^2$, or recognize directly that $-\sqrt{r^2-x^2}$ is an antiderivative of $\frac{x}{\sqrt{r^2-x^2}}$. This is easy to see, since earlier we differentiated $\sqrt{r^2-x^2}$.

Finally, plug in. We end up with $2\pi r^2$. And multiply by $2$, since we were calculating the surface area of the half-sphere.

Answer 2

Try this as an exercise in geometry. Show that if you fit a sphere into a cylinder just big enough to contain it, that the cylinder and the sphere have equal area. In other words, the projection of a sphere onto its containing cylinder is area preserving. I think that Archimedes did something similar.

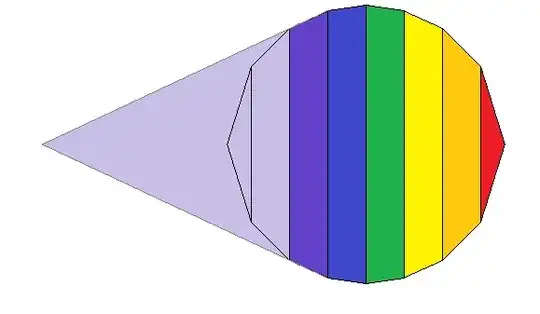
Note that we can approximate the surface area by fitting a series cones over the sphere. These cone segments are called frustums, and are used to find the area of almost any surface of revolution.

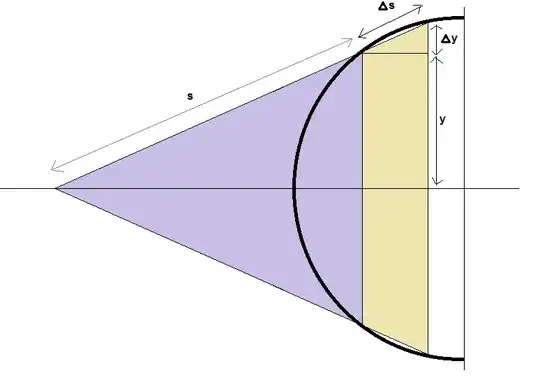
Normally, we represent the area of a cone as $\pi r s$, where $r$ is the radius of the base and $s$ is the distance from the vertex to the perimeter of the base. Now, this is where I do something a bit unusual. Instead of representing the arc length as $s$, I let $s$ represent the distance between where the tangent/secant line to the circle touches the circle and where it crosses the x-axis. $s$ now means something completely different, but $ds$ can be interpreted either as an inclined distance on the frustum or as a change in arc length, which is nice. So to find the area of the frustum we have: $$\pi(y+dy)(s+ds) - \pi ys = \pi (yds+sdy) +\pi dyds$$ But bear in mind to find the surface area, we integrate with respect to $x$ (i.e. we have a SINGLE integral). This means that I am not interested in the $dyds$ term because $\displaystyle\lim_{dx\to 0} \int_{-r}^{r}dyds = 0$.
So we have $$SA_{frustum}=\pi (yds + sdy)$$ But by similarity of the triangles in figure 3 (half the purple one and the small yellow one at the top) we have$\dots$ $$\frac{s}{y} = \frac{ds}{dy}$$ $$sdy = yds$$ so $$SA_{frustum} = 2\pi yds$$ Also noteworthy, is that I calculated $y'(x)$ implicitly $$x^2 + y^2 = r^2$$ $$2x + 2yy' = 0$$ $$y' = -x/y$$ and SA of the sphere becomes $$SA_{sphere}=\int_{x=-r}^{x=r} \pi(yds+sdy) = \int_{x=-r}^{x=r} 2\pi yds$$ $$\displaystyle= 2\pi\int_{x=-r}^{x=r}y\sqrt{1+(y'(x))^2}dx=2\pi\int_{x=-r}^{x=r}y\sqrt{1+(-x/y)^2}dx $$ $$=2\pi\int_{x=-r}^{x=r}y\sqrt{\frac{y^2+x^2}{y^2}}dx=2\pi\int_{x=-r}^{x=r}y\frac{r}{y}dx$$ $$=2\pi r\int_{x=-r}^{x=r}dx$$ $$=2\pi r\bigg|_{-r}^{r}x=2\pi r (r - (-r))=4\pi r^2$$

Answer 3

Note that the parametrization of sphere is given by $$r(u,v)=(r\sin u\cos v,r\sin u\sin v,r\cos u)$$ where $0\leq u\leq \pi$ and $0\leq v\leq2\pi.$ So the surface area is given by the formula $$\int_0^{2\pi}\int_0^{\pi}||r_u\times r_v|| du\hspace{1mm} dv$$ Now calculate the integral to get the formula.

Answer 4

I won't go into a proof that the surface of the sphere $S^2_r$ of radius $r$ is $4\pi r^2$.

Your last question asks for the area of a unit square on $S^2_r$. The notion "unit square" can mean two things: A "square" $Q\subset S^2_r$ of unit area, or a "square" $Q\subset S^2_r$ of unit side length. I guess you mean the latter.

Such a square $Q$ is the union of $8$ congruent rectangular spherical triangles $T$. Denote by $T'$ the corresponding triangle on the unit sphere $S^2$ obtained by scaling. One leg of $T'$ has length $a:={1\over 2 r}$, and the angle opposite to $a$ is $\alpha:={\pi\over 4}$. The third angle $\beta$ is related to $a$ and $\alpha$ via the following formula from spherical trigonometry: $$\cos\alpha=\cos a\sin\beta\ .$$ It follows that $$\beta=\arcsin{1\over\sqrt{2}\cos(1/(2r))}\ .$$ The area of $T'$ then computes to $${\rm area}(T')=\left(\alpha+\beta+{\pi\over2}\right)-\pi=\beta-{\pi\over4}\ ,$$ and finally we obtain the area of $Q$ as $${\rm area}(Q)=8r^2\>{\rm area}(T')\ .$$

Answer 5

Without integrals, albeit a little less rigorous:

Take half a sphere. Imagine to press it on a plane until it has become a circle.

Of course the surface area is still the same; what's the radius of the circle?

it is clearly $r\sqrt{2}$, where $r$ is the radius of the sphere (basically the points that were on the edge of the sphere (distance $r\sqrt{2}$ from the top of the sphere) now all lie on the circumference that has the top of the spere as its centre))

So the surface area of half a sphere is $2\pi r^2$, and of the whole sphere $4\pi r^2$.

Answer 6

Consider a cylinder radius R intersected by a triangular wedge or prism with length 2R width R thickness t: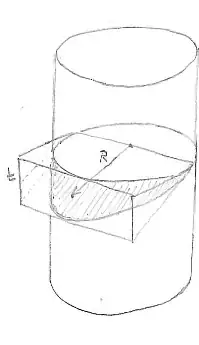

Calculate the area $S$ of the shaded portion by sweeping the arrow from the position shown through $\pi/2$, noting that the height of the shaded portion at angle $\theta$ is $t\cos\theta$ and the width of swept angle $\delta\theta$ is $R \delta\theta$

$$ S = 2 \int_{0}^{\pi/2} t\cos\theta Rd\theta $$ or $$ S = 2Rt ^{\dagger} $$

Now stack multiple trimmed wedges to form a spheroid:

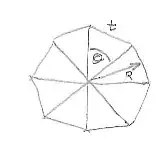
and sum the area of all the shaded portions as $t\rightarrow 0$ noting that $\delta t = R \delta\theta$

$$ A = \int_{0}^{2\pi} 2R R d\theta $$

or

$$ A = 4\pi R^2 $$

Or more directly $A = \int_{t=0}^{2\pi R} 2Rdt$

$\dagger$ this is the same as the area of the $2R\times t$ face of the wedge which leads to a simple proof that the surface area of a sphere is the same as that of its surrounding cylinder

Answer 7

Hint

Take the sphere to be formed by the rotation of semicircle(why?) about x-axis $ x = r \cos \theta $, $ y = r \sin \theta $ where $ \theta \in [0, \pi] $.