Visualization of surface area of a sphere

Question

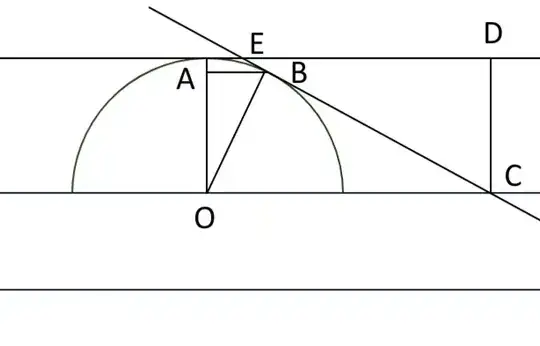
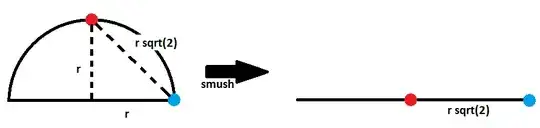
I help mentor some really young, bright kids in mathematics. We were looking at geometric properties of various shapes, and one of the kids noted that the surface area of a sphere $S = 4\pi r^2$ contains the equation for the area of a circle $A = \pi r^2$.

She was a bit confused why the factor of $4$ was mysteriously there. I told her I'd get back to her.

I know how to prove the formula using calculus, but I spent a long time trying to find an elementary way of doing it.

Does anyone know of a way of proving the first equation using almost no advanced mathematics$^1$? This seems unlikely, so as a separate question, does anyone know of a good visualization to show the relation between $S$ and $A$?

The naive approach of taking four circles and showing you can "place them" on a sphere is clearly wrong (you can't just place four circles on a sphere), but I'm not sure what the alternative is.

$^1$These kids have a working knowledge of variable manipulation, basic geometry, and I guess combinatorics?

Answer 1

One way to proceed is to make use of the well-known (well, it should be well-known) property of a sphere: If you inscribe a unit sphere within a right cylinder, and slice them "horizontally" (i.e., perpendicular to the axis of the cylinder) the corresponding strips of the sphere and of the cylinder have equal areas.

That this is true can be seen by examining the strips in the limit. Each strip of the sphere has smaller radius than the corresponding strip of the cylinder, by an amount equal to the cosine of the "latitude" of the strip, but by the same token, the sphere's strip is wider than the corresponding strip of the cylinder, by an amount equal to the secant of the latitude. The two factors cancel each other out.*

Since the entire cylinder, neglecting the ends (which don't correspond to any portion of the sphere), has height $2$ and circumference $2\pi$, its area—and therefore the area of the sphere—is $2 \times 2\pi = 4\pi$.

---

*We prove that the projection ratios cancel out without triginometric functions. In the illustration below the center of the semicircle us at O, the lines OC, AB and ED are parallel, OA and DE are perpendicukar to those lines, and ED and the transversal EC are tangent to the semicircle. Then use the fact that parallel lines generate congruent alternate interior angles; thereby the corresponding angles of right $\triangle$s OBA and ECD are congruent and the triangles are similar. Thus |AB|/|OB|=|DC|/|CE| and the required cancellation of projection ratios follows.

Answer 2

I just got done teaching the class again and it went extremely well, so I wanted to post my methods here. This isn't technically an answer, but more of what I did which works as an answer.

All credit for my fundamental idea goes to @dxiv and the link he posted in the comment to my question.

---

I gave each kid half of a cored orange (essentially a hemisphere) and told them to use it as a stencil to trace out a circle. They determined the radius of this first circle to be $1.6 \text{ inches}$.

I argued that the surface area is a measure of how much paint we'd need to cover the top of the half-orange. I then argued that if we smushed the orange into a flat disk, the amount of paint we need obviously wouldn't change (if we painted every point pre-smush, no point would be unpainted post-smush), so the surface area wouldn't change.

They smushed the orange and, again, used it as a stencil to trace out a circle. They found the radius of this circle to be $2.25 \text{ inches}$.

The area of our original circle, $\pi r^2$, is about $8 \text{ inches}^2$. The area of our new circle is about $16 \text{ inches}^2$. So, the surface area of the hemisphere is $2\pi r^2$, and the surface area of the full sphere is $4\pi r^2$.

They were extremely happy with this demonstration, but I obviously wasn't - it wasn't quite rigorous. So to round out the lesson, I showed them the following diagram (reproduced here in Paint):

Under the smush operation, I said that the distance between the red and blue points should not change. This would mean that our second circle should have a radius that is off by a factor of $\sqrt2$ from our first circle. Lo and behold:

$$1.6\sqrt2 \approx 2.25$$

They all left pretty satisfied, so I think the demonstration worked, sans the fact it was a bit hand-wavy.

Answer 3

This is definitely not an answer, but if you intend to use the "four parts of an orange peel" analogy, this might be relevant.

This might be entertaining for some, especially those who enjoy confusing people with numerical coincidences (like Randall Munroe's XKCD comics 217 and 1047).

I was thinking about the regular simplex in 3D -- the regular tetrahedron.

If you put a regular tetrahedron inside the unit sphere, i.e with the four vertices of the tetrahedron on the unit sphere, the six edges of the tetrahedron are $\sqrt{8/3}$. Each of the four faces is an equilateral triangle (each side being, of course, said $\sqrt{8/3}$). The area of each triangular face is therefore $\sqrt{4/3} = 2/\sqrt{3}$.

The area of the unit sphere is $4\pi$, so the area of each triangular quadrant on the unit sphere -- as if the tetrahedron was puffed up into a sphere -- is $\pi$.

(The edges of each puffed-up face is an arc of a great circle.)

The ratio between the area of the unit sphere quadrant and the tetrahedral faces is $\pi:2/\sqrt{3} \approx 2.72070$, which is within one thousandth of $e \approx 2.71828$.
(With three significant digits, both round to $2.72$.)

This is a coincidence; the ratios in lower and higher number of dimensions is quite different.

Answer 4

Reading @NominalAnimal 's informative nonanswer suggests this almost answer.

I would start thinking about spherical trigonometry with your fifth graders. Examples show that the sum of the angles of a triangle is always greater than $\pi$ (radian measure, of course, which you've introduced if they don't know it). Then motivate Girard's Theorem - the area of a spherical triangle is the spherical excess: the sum of the angles - $\pi$.

Then each of the four spherical triangles that you get by blowing up the inscribed tetrahedron has area $\pi$, so the area of the sphere is $4\pi$.

This isn't quite a proof, because you may need to use the area of the the sphere to prove Girard's Theorem, but it is an interesting digression and an intuitive argument.

I hang out with some good fifth graders and think this is well worth doing. I will try it in the fall.

Answer 5

I think the idea of trying to do this without calculus is misguided. Instead, try to understand the steps in the calculus. The surface area formula is derived from the volume formula so maybe the question should be: can I get the volume formula from the formula for circle area $A_c=\pi r^2$? First, break down the sphere into disks (centered on the x-axis). Then using cylinder volumes we have: $$V=\int_{-r}^{r}\pi(r^2-x^2)dx=\frac{4}{3}\pi r^3$$ We can do this because for cylinder volume $V=\pi R^2h$ where $h$ is height $R=y$ and so $R^2=y^2=r^2-x^2$. To understand how this relates to the surface area consider the end of the FTC proof, which goes like this: $$\frac{dA}{dx}=y$$ $$dA=y·dx$$ $$A=\int y·dx$$ where $A$ is the area function for $y$. Comparing the above equation to the previous integral we can see that we should be able to differentiate $V$ to produce something equivalent to $y$ i.e. something that encompasses and spatially defines itself. What could that be for the volume? It would have to be the surface area!