Intuition for sum of triangular numbers and significance for $3\choose{k}$

Question

Specific question: according to my calculation based on Timbuc's answer to this question,

$$\sum_{k=0}^n\frac{k(k+1)}{2}=\frac{n(n+1)(2n+4)}{12} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; =\frac{n(n+1)(n+2)}{6}$$

[Edit: RHS simplified based on suggestion from herbsteinberg.]

If this is right, is there an intuitive or geometric proof of this?

Background and motivation: I'm trying to relate the concepts of integration and summation using reasoning which I find simple and intuitive.

As part of that, I'm trying to understand the process of summing sequences in this rotated section of Pascal's triangle:

$(0)\;\;01\;\;01\;\;01\;\;01\;\;01\;\;01\;\;...\frac{k^0}{0!} \\ (1)\;\;01\;\;02\;\;03\;\;04\;\;05\;\;06\;\;...\frac{k+0}{1!} \\ (2)\;\;01\;\;03\;\;06\;\;10\;\;15\;\;21\;\;...\frac{k(k+1)}{2!} \\ (3)\;\;01\;\;04\;\;10\;\;20\;\;35\;\;56\;\;...\frac{k(k+1)(k+2)}{3!}$

I see that summing each line seems to increase the degree of the expression by $1$ and I can imagine that rearrangement, simplification and/or a limit process could later reduce these terms to $\frac{k^2}{2}$, $\frac{k^3}{3}$ etc., but for now I'm interested in how/why each line has the exact expression it does.

Line $(1)$ is just counting.

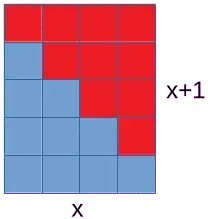
Line $(2)$ I can picture and understand as in Fig. 1 below.

Fig. 1

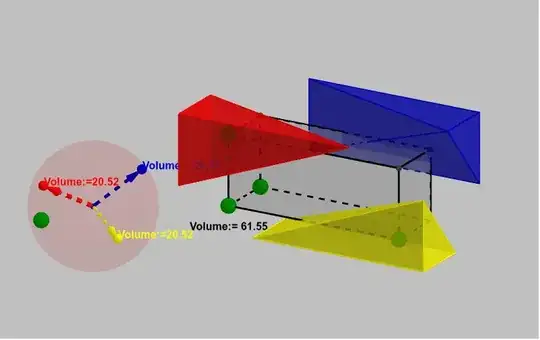
Line $(3)$ [Edited to add the following, which may start to answer my question] I can picture and understand as a stepped version of the right-angled tetraga in Fig. 2 below.

Fig. 2

Answer 1

Intuitively, you are walking the pascal triangle, in a zigzag way.

$$\binom{n}{k} + \binom{n}{k-1} = \binom{n+1}{k}$$

For your example, $\large \sum_{k=0}^{n}{k(k+1)\over 2} = \sum_{k=1}^{n}\binom{k+1}{2} = \binom{n+2}{3}$

$$\large\begin{matrix} \binom{2}{2} = \binom{3}{3} = 1 \cr \binom{3}{3} + \binom{3}{2} = \binom{4}{3} = 4 \cr \binom{4}{3} + \binom{4}{2} = \binom{5}{3} = 10 \cr \binom{5}{3} + \binom{5}{2} = \binom{6}{3} = 20 \cr \cdots \cr \Large\binom{n+1}{3} + \binom{n+1}{2} = \binom{n+2}{3} \end{matrix}$$

Answer 2

Inspired by Sum of Consecutive Squares Formula Proof $$S_n = \sum_{k=1}^n\binom{k+1}{2}$$ $$3S_4 = \begin{matrix} 1 && 1 && 4\cr 12 && 21 && 33\cr 123 &+& 321 &+& 222\cr 1234 &&4321 && 1111\cr \end{matrix}$$

$3S_4 = \begin{matrix} 6\cr 66\cr 666\cr 6666 \end{matrix}$

$6S_4 = \begin{matrix} 66666\cr 66666\cr 66666\cr 66666 \end{matrix}$

$$S_4 = {4(4+1)(4+2) \over 6}$$ $$→ S_n = {n(n+1)(n+2) \over 6}$$

Answer 3

Each row can be written as a sum of combinatorial numbers. This is what is known as the Hockey Stick Identity

A nice way of imaginining the intuition behind these identities is understanding a combinatorial proof for the hockey stick identity