First: the given series is not Cesaro- or Abel-summable.
For the Abel-summability we would make the ansatz
$$ \lim_{x \to \;^-1} 1+3x+6x^2+\cdots+\binom{k+2}{2}x^k+ \cdots \underset{\mathcal A}= { 1\over(1-x)^3}\underset{\mathcal A}=+\infty
$$
$\qquad \qquad \qquad \qquad \qquad \qquad \qquad $ $\mathcal A$ indicating Abel-summation for divergent series
Second: if one looks for alternatives, then
shifting the index might come to mind, such that we might try
$$ \begin{array}{} &S_2&= &1+3+6+10+... \\
&&\underset{??}=& 1+2+3+4+... \\
&&&+0+1+3+6+... \\
&&\underset{??}=& S_1 + S_2 \qquad \qquad \qquad && &\text{where }S_1=1+2+3+4+... \\
\implies& 0 &=& S_1 &&& \text{and no information for $S_2$}
\end{array}
$$
which makes such an idea worthless.
Third: a more meaningful ansatz is surely the following.
(This has already been proposed by Daniel Fischer, but I repeat this here to show the nice generalization)
By this we avoid the idea of any shifting of the index at all and formulate
$$ S_2(s) = {1\over 1^s} + {3\over 2^s} + {6\over 3^s} + \cdots + {\binom{k+1}2\over k^s}+\cdots = \sum_{k=1}^\infty {\binom{k+1}2\over k^s}
$$
which gives convergent series for all $s>3$ We can then observe (and prove, of course) that for the whole continuous range of convergence
$$ \begin{array}{} 2 S_2(s) &=& {2\over 1^s} + {6\over 2^s} + {12\over 3^s} + \cdots \\
&=& {1\over 1^s} + {2\over 2^s} + {3\over 3^s} + \cdots \\
&+& {1^1\over 1^s} + {2^2\over 2^s} + {3^2\over 3^s} + \cdots \\
&=& \sum_{k=1}^\infty { 1\over k^{s-1}} + \sum_{k=1}^\infty { 1\over k^{s-2}} \\
&=& 1 \cdot \zeta(s-1) + 1 \cdot \zeta(s-2)
\end{array}$$
It must be taken from elsewhere, that we can extend this summation-expression beyond range of convergence, towards
$$ S_2 = \lim_{s \to 0} \frac12 (1 \cdot \zeta(s-1)+ 1 \cdot \zeta(s-2))\underset{\mathcal Z}= \frac12 \cdot( - \frac1{12}+ 0) = -\frac1{24}
$$
I found it much interesting, how this could be generalized for series of binomials of higher order.
We get this way
$$ \begin{array}{}
S_1 &=& \sum_{k=1}^\infty \binom{k}{1} &\underset{\mathcal Z}=&1 \cdot \zeta(-1) \\
S_2 &=& \sum_{k=1}^\infty \binom{k+1}{2}& \underset{\mathcal Z}=\frac1{2!} (&1 \cdot \zeta(-1) + 1 \cdot \zeta(-2) )\\
S_3 &=& \sum_{k=1}^\infty \binom{k+2}{3} &\underset{\mathcal Z}=\frac1{3!} (&2 \cdot \zeta(-1) + 3 \cdot \zeta(-2) + 1 \cdot \zeta(-3) )\\
S_4 &=& \sum_{k=1}^\infty \binom{k+3}{4} &\underset{\mathcal Z}=\frac1{4!} (&6 \cdot \zeta(-1) + 11 \cdot \zeta(-2) + 6 \cdot \zeta(-3) + 1 \cdot \zeta(-4))\\
\vdots & & \vdots
\end{array}$$
where your series occurs as
$S_2$.
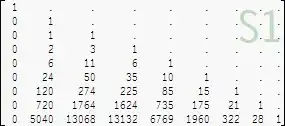
Heuristically I found the coefficients applying multiple regression (I can show this simple procedure if requested), and finally found, that those coefficients at the $\zeta(-k)$s are the unsigned Stirlingnumbers first kind.
Displayed in a matrix (top-left from the infinite array):