Summation of fractional parts of $x/n$

Question

Let us consider the sums $$\displaystyle T_1(x)=\sum_{n\geq a\sqrt{x}}^{b \sqrt{x}} \left\{ \frac{x}{n} \right\} \\T_2(x)=\sum_{n\geq a\sqrt{x}}^{b \sqrt{x}} \left\{ \frac{x}{2n} \right\} $$ where $x$ is a positive integer, $0\leq a<b\leq 1$, $n$ runs over all integers in the interval $[a \sqrt{x}, b\sqrt{x}]$, and $\{ \}$ indicates the fractional part. Because of the equidistribution of such fractional parts, the plots of $T_1(x)$ and $T_2(x)$ versus $x$ show oscillations around the line $\frac{b-a}{2} \sqrt{x}$.

By experimental calculations, I noted that the average value of the difference between $T_1(x)$ (or $T_2(x)$) and $\frac{b-a}{2} \, \sqrt{x}$, calculated over all positive integers $x \leq N$, is $O(1)$. In particular, we have

$$\lim_{N \rightarrow \infty} \frac{1}{N} \sum_{x=1}^{N} \left( T_1(x)- \frac{b-a}{2} \sqrt{x} \right)= K_1(a,b)\\ \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{x=1}^{N} \left( T_2(x)- \frac{b-a}{2} \sqrt{x} \right)= K_2(a,b)$$

where $K_1(a,b)$ and $K_2(a,b)$ are constant terms that depend on $a$ and $b$, indicating that the distributions of such differences are biased.

The problem can be simplified by considering the case where $b=1$ (once solved this case, the general case with $b<1$ can be solved by difference). In this case, the biases are determined only by $a$. For example, analyzing the distributions of differences over all integers $N$ up to $2500$, setting $a=0.5$ we have $K_1(0.5,1)\approx -0.370...$ and $K_2(0.5,1)\approx -0.169...$, with rather slow convergence rates. I wonder how these terms are generated and whether they could be exactly calculated. Again based on experimental results, it seems that $K_1$ and $K_2$ have a logarithmic relation with $a$, with values near to $\frac{1}{2} \log(a)$ and $\frac{1}{4} \log(a)$, respectively.

This question is somewhat linked to this other one, for which a nice answer was previously given.

EDIT (after Mathworker21's answer): A rough numerical computation until $N=10000$ for the case $a=0.5$, $b=1$ seems to confirm the above estimates obtained with $N$ up to $2500$. Here is the plot of the differences $T_1(x)- \frac{b-a}{2} \sqrt{x}$ versus $x$, followed by that of the average value of these differences calculated over the first $N$ integers. As show in this second plot, $K_1(0.5,1)$ seems to converge to $\approx -0.37$. The dotted black line in the first graph is the best fitting line, whose intercept is compatible with such value. Based on a visual assessment, large departures from this value (as suggested by the provided answer) for higher $N$ seem unlikely:

Similar considerations can be made for $K_2(0.5,1)$, which seems to converge to $\approx -0.17$:

Answer 1

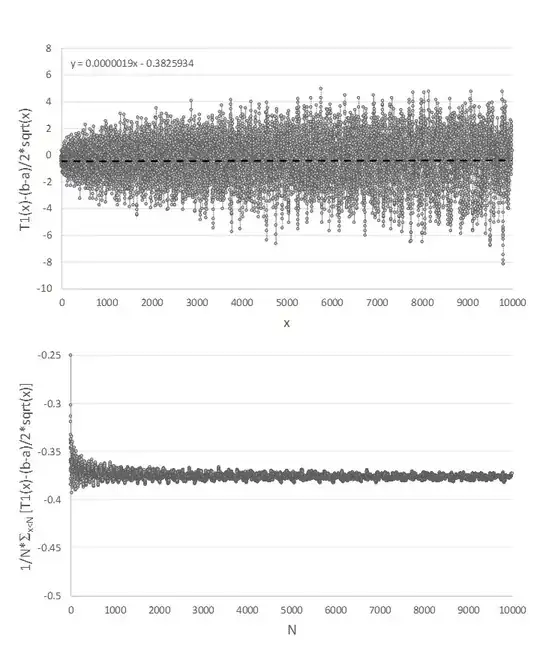
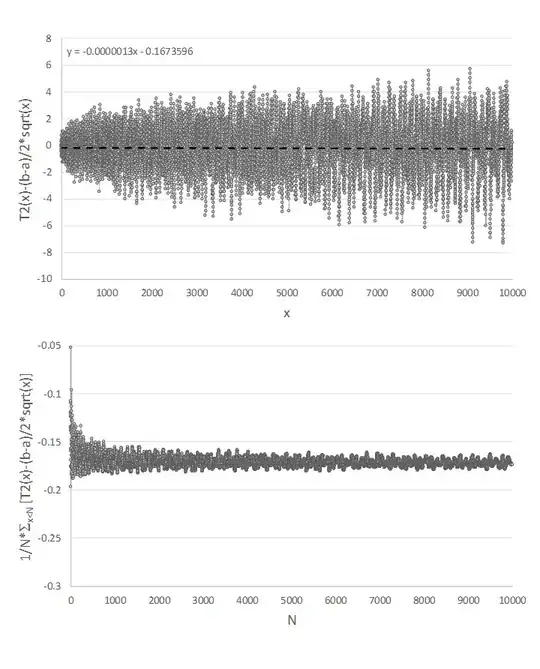
We show $K_1(a,b) = -\frac{b^2-a^2}{24}-\frac{1}{2}\log(b/a)$. $K_2(a,b)$ can be found using the same methods used below.

The starting point is the identity $$\{\theta\}-\frac{1}{2} = \frac{-1}{\pi}\sum_{n=1}^\infty \frac{\sin(2\pi n\theta)}{n},$$ valid for $\theta \not \in \mathbb{Z}$ [Thanks to metamorphy for pointing out the invalidity for $\theta \in \mathbb{Z}$, and Anatoly for pointing it out again]. We show later that $$\lim_{N \to \infty} \frac{1}{N}\sum_{x=1}^N \sum_{\substack{m = a\sqrt{x} \\ m \mid x}}^{b\sqrt{x}} (\{\frac{x}{m}\}-\frac{1}{2}) = -\frac{1}{2}\log(b/a).$$

Using the fourier identity above, we obtain $$\frac{1}{N}\sum_{x=1}^N \sum_{\substack{m=a\sqrt{x} \\ m \not \mid x}}^{b\sqrt{x}} \left(\{\frac{x}{m}\}-\frac{1}{2}\right) = \frac{1}{N}\sum_{x=1}^N\sum_{m=a\sqrt{x}}^{b\sqrt{x}} \frac{-1}{\pi}\sum_{n=1}^\infty \frac{\sin(2\pi nx)}{n}.$$ For ease, we dropped the condition "$m \not \mid x$", which is allowed, since $\sin(2\pi n\frac{x}{m}) = 0$ if $m \mid x$. Since the outer two sums are finite, we may interchange to get $$\frac{-1}{\pi}\sum_{n=1}^\infty \frac{1}{n}\sum_{m=1}^{b\sqrt{N}}\frac{1}{N}\sum_{x=m^2/b^2}^{\min(m^2/a^2,N)} \sin(2\pi \frac{n}{m}x).$$ Suppose that $\frac{1}{a^2}$ and $\frac{1}{b^2}$ are integers, for ease. Using the identity $$\sin(\theta)+\dots+\sin(k\theta) = \frac{\cos(\frac{\theta}{2})-\cos((k+\frac{1}{2})\theta)}{2\sin(\frac{\theta}{2})},$$ we see that $$\sum_{x=m^2/b^2}^{m^2/a^2} \sin(2\pi\frac{n}{m}x) = \frac{1}{2\sin(\pi\frac{n}{m})}\left[\cos\left((\frac{m^2}{b^2}-1+\frac{1}{2})2\pi \frac{n}{m}\right)-\cos\left((\frac{m^2}{a^2}+\frac{1}{2})2\pi\frac{n}{m}\right)\right]$$ and $$\sum_{x=m^2/b^2}^N \sin(2\pi \frac{n}{m}x) = \frac{1}{2\sin(\pi\frac{n}{m})} \left[\cos\left((\frac{m^2}{b^2}-1+\frac{1}{2})2\pi\frac{n}{m}\right)-\cos\left((N+\frac{1}{2})2\pi\frac{n}{m}\right)\right].$$ Using again that $\frac{1}{a^2}$ and $\frac{1}{b^2}$ are integers, $$\cos\left((\frac{m^2}{b^2}-1+\frac{1}{2})2\pi \frac{n}{m}\right)-\cos\left((\frac{m^2}{a^2}+\frac{1}{2})2\pi\frac{n}{m}\right) = \cos\left(\frac{\pi n}{m}\right)-\cos\left(\frac{\pi n}{m}\right) = 0$$ and $$\cos\left((\frac{m^2}{b^2}-1+\frac{1}{2})2\pi\frac{n}{m}\right)-\cos\left((N+\frac{1}{2})2\pi\frac{n}{m}\right) = \cos\left(\frac{\pi n}{m}\right)-\cos\left(\frac{\pi n}{m}+2\pi\frac{N n}{m}\right).$$ Note that $$\cos(\frac{\pi n}{m}+2\pi\frac{N n}{m}) = \cos(\frac{\pi n}{m})\cos(2\pi\frac{N n}{m})-\sin(2\pi \frac{N n}{m})\sin(\frac{\pi n}{m}).$$ Putting everything together, $$\frac{1}{N}\sum_{x=1}^N \sum_{m=a\sqrt{x}}^{b\sqrt{x}} \left(\{\frac{x}{m}\}-\frac{1}{2}\right) = \frac{-1}{\pi}\sum_{n=1}^\infty \frac{1}{n}\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{\cos(\frac{\pi n}{m})[1-\cos(2\pi \frac{N n}{m})]+\sin(\frac{\pi n}{m})\sin(2\pi \frac{N n}{m})}{2\sin(\frac{\pi n}{m})}.$$ We handle the term $$\frac{-1}{\pi}\sum_{n=1}^\infty \frac{1}{n}\frac{1}{2N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \sin(2\pi \frac{N n}{m}) = \frac{1}{2N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \left(\{\frac{N}{m}\}-\frac{1}{2}\right) \to 0$$ as $N \to \infty$. Now, using $1-\cos(2\theta) = 2\sin^2(\theta)$, we are left with $$\frac{1}{N}\sum_{x=1}^N \sum_{m=a\sqrt{x}}^{b\sqrt{x}} \left(\{\frac{x}{m}\}-\frac{1}{2}\right) = \frac{-1}{\pi}\sum_{n=1}^\infty \frac{1}{n}\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{\sin^2(\pi \frac{N n}{m})\cos(\pi \frac{n}{m})}{\sin(\pi \frac{n}{m})}.$$ Let $$c_{n,N} = \frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{\sin^2(\pi\frac{Nn}{m})\cos(\frac{\pi n}{m})}{\sin(\frac{\pi n}{m})}.$$ We prove afterwards that, for any fixed $n$, $$\lim_{N \to \infty} c_{n,N} = \frac{1}{n}\frac{b^2-a^2}{4\pi}.$$ Using $$\lim_{N \to \infty} \frac{-1}{\pi}\sum_{n=1}^\infty c_{n,N} = \frac{-1}{\pi}\sum_{n=1}^\infty \lim_{N \to \infty} c_{n,N},$$ which we justify later, we finally obtain $$\frac{1}{N}\sum_{x=1}^N \sum_{\substack{m=a\sqrt{x} \\ m \not \mid x}}^{b\sqrt{x}} \left(\{\frac{x}{m}\}-\frac{1}{2}\right) = \frac{-1}{\pi}\sum_{n=1}^\infty \frac{1}{n^2}\frac{b^2-a^2}{4\pi} = -\frac{b^2-a^2}{24}.$$

---

We first show $$\lim_{N \to \infty} \frac{1}{N}\sum_{x=1}^N \sum_{\substack{m = a\sqrt{x} \\ m \mid x}}^{b\sqrt{x}} (\{\frac{x}{m}\}-\frac{1}{2}) = -\frac{1}{2}\log(b/a).$$ Of course, $\{\frac{x}{m}\} = 0$ if $m \mid x$. Interchanging summations, $$\frac{1}{N}\sum_{x=1}^N \sum_{\substack{m=a\sqrt{x} \\ m \mid x}}^{b\sqrt{x}} 1 = \frac{1}{N}\sum_{m=1}^{a\sqrt{N}} \sum_{\substack{m^2/b^2 \le x \le m^2/a^2 \\ m \mid x}} 1 + \frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \sum_{\substack{m^2/b^2 \le x \le N \\ m \mid x}} 1.$$ $$ = \frac{1}{N}\sum_{m=1}^{a\sqrt{N}} [\frac{m}{a^2}-\frac{m}{b^2}+O(1)]+\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} [\lfloor \frac{N}{m}\rfloor -\frac{m}{b^2}+O(1)] = \log(b/a)+O(\frac{1}{\sqrt{N}}).$$

We now prove that, for any fixed $n \ge 1$, $$\lim_{N \to \infty} \frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{\sin^2(\pi\frac{N n}{m})\cos(\frac{\pi n}{m})}{\sin(\frac{\pi n}{m})} = \frac{1}{n}\frac{b^2-a^2}{4\pi}.$$ As $\cos(\frac{\pi n}{m}) = 1+O(\frac{1}{m^2})$, and $\sin^2(\pi \frac{N n}{m}) \le 1$ and $\sin(\frac{\pi n}{m}) \gtrsim \frac{1}{m}$, we may replace $\cos(\frac{\pi n}{m})$ by $1$. Similarly, since $\sin(\frac{\pi n}{m}) \ge \frac{\pi n}{m}-c\frac{\pi^3}{n^3}{m^3}$, we may replace $\sin(\frac{\pi n}{m})$ by $\frac{\pi n}{m}$. We are left with $$\frac{1}{\pi n}\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} m\sin^2\left(\pi \frac{N n}{m}\right).$$ Using again that $\sin^2(\theta) = \frac{1-\cos(2\theta)}{2}$, it suffices to show $$\frac{1}{N}\sum_{n=a\sqrt{N}}^{b\sqrt{N}} m\cos(2\pi\frac{N n}{m}) \to 0.$$ It clearly then suffices to show $$\frac{1}{N}\sum_{m=1}^{c\sqrt{N}} m\cos(2\pi \frac{N n}{m}) \to 0$$ for any fixed $c \in (0,1)$. By summation by parts, $$\frac{1}{N}\sum_{m=1}^{c\sqrt{N}} m\cos(2\pi \frac{N n}{m}) = \frac{1}{N}(c\sqrt{N})\sum_{m=1}^{c\sqrt{N}} \cos(2\pi \frac{N n}{m}) - \frac{1}{N}\int_1^{c\sqrt{N}} \left[\sum_{m \le t} \cos(2\pi \frac{N n}{m})\right]dt,$$ so it suffices to show some nontrivial amount of equidistribution of $\{\frac{N n}{m}\}$ for $m \le c\sqrt{N}$, which shouldn't be too bad.

Now we handle $K_2(a,b)$. We show that $K_2(a,b) = -\frac{b^2-a^2}{12}-\frac{1}{4}\log(b/a)$ if $\frac{1}{a^2},\frac{1}{b^2}$ are integers of the same parity. This can be extended to the case of $\frac{1}{a^2},\frac{1}{b^2}$ any integers. Take, for example, $a = \frac{1}{2}, b = 1$. For any $k \ge 1$, we have $$K_2(\frac{1}{2},1) = K_2(\frac{1}{3},1)-K_2(\frac{1}{4},\frac{1}{2})+K_2(\frac{1}{5},\frac{1}{3})-K_2(\frac{1}{6},\frac{1}{4})+\dots+K_2(\frac{1}{2k+1},\frac{1}{2k-1})-K_2(\frac{1}{2k+1},\frac{1}{2k}).$$ Since $K_2(\frac{1}{2k+1},\frac{1}{2k}) \le K_2(\frac{1}{2k+1},\frac{1}{2k-1})$ can be made arbitrarily small, we get, after a brief computation, $K_2(\frac{1}{2},1) = -\frac{1-.5^2}{12}-\frac{1}{4}\log(1/.5)$.

Similar to before, $$\frac{1}{N}\sum_{x=1}^N \sum_{\substack{m \ge a\sqrt{x} \\ 2m \mid x}}^{b\sqrt{x}} 1 = \frac{1}{N}\sum_{m=1}^{a\sqrt{N}}\sum_{\substack{m^2/b^2 \le x \le m^2/a^2 \\ 2m \mid x}} 1 + \frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \sum_{\substack{m^2/b^2 \le x \le N \\ 2m \mid x}} 1$$ $$= \frac{1}{N}\sum_{m=1}^{a\sqrt{N}} \frac{m}{2}(\frac{1}{a^2}-\frac{1}{b^2})+\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{N-\frac{m^2}{b^2}}{2m} = \frac{1}{2}\log(b/a)+O(\frac{1}{N}).$$ Therefore, $$\frac{1}{N}\sum_{x=1}^N \sum_{\substack{m \ge a\sqrt{x} \\ 2m \mid x}} \left(\{\frac{x}{2m}\}-\frac{1}{2}\right)$$ contributes a $\frac{-1}{4}\log(b/a)$. As before, we do $$\frac{1}{N}\sum_{x=1}^N \sum_{\substack{m \ge a\sqrt{x} \\ 2m \not \mid x}}^{b\sqrt{x}} \frac{-1}{\pi}\sum_{n=1}^\infty \frac{\sin(2\pi n \frac{x}{2m})}{n}.$$ Dropping the condition "$2m \not \mid x$" (which is permissible), interchanging sums, and using the sum-of-sines formula again, and noting that $$\cos\left((\frac{m^2}{b^2}-\frac{1}{2})\pi \frac{n}{m}\right)-\cos\left((\frac{m^2}{a^2}+\frac{1}{2})\pi\frac{n}{m}\right) = 0$$ since $\frac{1}{b^2},\frac{1}{a^2}$ are even, we obtain $$\frac{-1}{\pi}\sum_{n=1}^\infty \frac{1}{n} \frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{\cos(\frac{\pi n}{2m})-\cos(N \pi \frac{n}{m})\cos(\frac{\pi n}{2m})+\sin(N \pi \frac{n}{m})\sin(\frac{\pi n}{2m})}{2\sin(\frac{\pi n}{2m})}.$$ As before, $$\frac{1}{2}\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{-1}{\pi}\sum_{n=1}^\infty \frac{\sin(N\pi \frac{n}{m})}{n} = \frac{1}{2}\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \left(\{\frac{N}{2m}\}-\frac{1}{2}\right) \to 0.$$ As before, we should have $$\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{\cos(N\pi \frac{n}{m})\cos(\frac{\pi n}{2m})}{\sin(\frac{\pi n}{2m})} \to 0$$ as $N \to \infty$ for any fixed $n \ge 1$. And, for any fixed $n \ge 1$, as $N \to \infty$, we have $$\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{\cos(\frac{\pi n}{2m})}{2\sin(\frac{\pi n}{2m})} \to \frac{1}{n}\frac{b^2-a^2}{2\pi},$$ so $$\frac{1}{N}\sum_{x=1}^N\sum_{\substack{m = a\sqrt{x} \\ 2m \not \mid x}}^{b\sqrt{x}} \left(\{\frac{x}{2m}\}-\frac{1}{2}\right) = -\frac{b^2-a^2}{12}.$$

Answer 2

Sigh, I hate fourier analysis. It turns people (especially me) into mindless, computing zombies.

The way to obtain $K_1(a,b)$ is literally just to interchange sums. I don't know why I didn't see this days ago. I don't have a fully rigorous proof, but I think it's just as rigorous as the fourier argument given in the other answer. This answer shows that $K_k(a,b) = \frac{-1}{2k}\log(\frac{b}{a})-\frac{k}{24}(b^2-a^2)$.

The intuitive reason the $\log$ appears is that $\frac{1}{2}$ is not the average value of $\{\frac{x}{m}\}$ for fixed $m$ as $x$ ranges. Instead, the average is $\frac{1}{m}\left[0+\frac{1}{m}+\dots+\frac{m-1}{m}\right] = \frac{m-1}{2m} = \frac{1}{2}-\frac{1}{2m}$. This "$\frac{-1}{2m}$" is the reason for the log. The reason for the $-\frac{k}{24}(b^2-a^2)$ is a bit harder to directly understand.

We assume $\frac{1}{a^2},\frac{1}{b^2}$ are integers that have the same residue modulo $k$. The result for any $a,b$ such that $\frac{1}{a^2}$ and $\frac{1}{b^2}$ are integers follows from an easy extension (to $k > 2$) of the reasoning given in the other answer.

$$\frac{1}{N}\sum_{x=1}^N \sum_{m=a\sqrt{x}}^{b\sqrt{x}} \left(\{\frac{x}{km}\}-\frac{1}{2}\right) = \frac{1}{N}\sum_{m=1}^{a\sqrt{N}}\sum_{x=m^2/b^2}^{m^2/a^2}\left(\{\frac{x}{km}\}-\frac{1}{2}\right)+\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}}\sum_{x=m^2/b^2}^N \left(\{\frac{x}{km}\}-\frac{1}{2}\right)$$ Since we repeatedly cycle through the residues mod $km$, the first term is $$\frac{1}{N}\sum_{m=1}^{a\sqrt{N}} \frac{-1}{2}\left(\frac{\frac{m^2}{a^2}-\frac{m^2}{b^2}}{km}+O(1)\right) = \frac{-1}{4k}\left(1-\frac{a^2}{b^2}\right)+O\left(\frac{1}{\sqrt{N}}\right)$$ For each $m$, writing $N = q_m km+r_m$ for $0 \le r_m \le km-1$, the second term is $$\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}}\sum_{x=m^2/b^2}^{q_m km} \left(\{\frac{x}{km}\}-\frac{1}{2}\right) + \frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \sum_{x=q_m km+1}^{q_m km+r_m} \left(\{\frac{x}{km}\}-\frac{1}{2}\right)$$ $$ = \frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{-1}{2}\left(q_m-\frac{m}{b^2k}+O(1)\right) + \frac{1}{N}\sum_{a=\sqrt{N}}^{b\sqrt{N}} \left[\left(\frac{1}{km}-\frac{1}{2}\right)+\dots+\left(\frac{r_m}{km}-\frac{1}{2}\right)\right]$$ $$ = \frac{-1}{2k}\log(b/a)+\frac{1}{4k}(1-\frac{a^2}{b^2})+\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \left(\frac{r_m(r_m+1)}{2km}-\frac{r_m}{2}\right)$$ The sum can be written as $$\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{mk}{2}(\frac{r_m}{km})^2-\frac{mk}{2}(\frac{r_m}{mk}),$$ and since $\frac{r_m}{mk} = \{\frac{N}{mk}\}$ should be equidistributed, and since $\int_0^1 x^2-x dx = \frac{-1}{6}$, we heuristically get $$\frac{1}{N}\sum_{m=a\sqrt{N}}^{b\sqrt{N}} \frac{mk}{2}(-\frac{1}{6}) = \frac{-k}{24}(b^2-a^2).$$ Putting everything together gives the desired $$\lim_{N \to \infty} \frac{1}{N}\sum_{x=1}^N \sum_{m=a\sqrt{x}}^{b\sqrt{x}} \left(\{\frac{x}{km}\}-\frac{1}{2}\right) = \frac{-1}{2k}\log\left(\frac{b}{a}\right)-\frac{k}{24}\left(b^2-a^2\right).$$