1

I am reading a book and current I am doing some exercises. The exercise that I am having trouble with is this:

Solve the following equation for $z$:

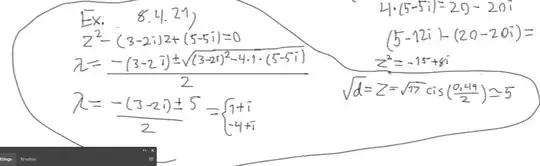
$z^2-(3-2i)z+(5-5i)=0$

I know that the solution is $2+i$ and $1-3i$ but I do not know the steps to get to this result. I have tried using the polar form of complex number to calculate the roots using the solution formula for quadratic equations. However, what I get is not even near the correct results :/

So if anyone could give a user-friendly walkthrough of how to solve that quadratic polynomial - I would be very very happy!

Oh, and here is my general results, if you manage to read it :P

enter image description here

user1551
  • 139,064
That Guy
  • 1,309
  • 3
    Using the quadratic formula should give you the correct results. Can you post the results you get by using it? – Leo Aug 19 '19 at 17:29
  • I just posted my drawings - and my results are $1+i$ and $-4+i$ :) – That Guy Aug 19 '19 at 17:34
  • Square roots of $-15+8i$ are wrong in your solution. To find them properly, you can follow the steps in https://math.stackexchange.com/questions/3042441/find-all-the-solutions-of-z2-13iz-8-i-0/3042458#3042458 – user376343 Aug 19 '19 at 17:40
  • Pleas refer to another answer of mine here. – Ng Chung Tak Aug 19 '19 at 19:28

5 Answers5

4

Consider in $\mathbb C[z]$ the equation $$az^2+bz+c=0.$$ As in $\mathbb R[z]$, the solutions are given by $$z_{1,2}=\frac{-b\pm\sqrt{\Delta }}{2a},$$ where $\Delta =b^2-4ac.$

Surb
  • 55,662
2

Use that your equation can be written as $$(z-(2+i)) (z-(1-3 i))$$

Dr. Sonnhard Graubner
  • 95,283
1

Let’s complete the square: $$(z^2-(3-2i)z+\left(\dfrac{3-2i}{2}\right)^2=\left(\dfrac{3-2i}{2}\right)^2-(5-5i).$$ This gives us $$\left(z-\dfrac{3-2i}{2}\right)^2=\dfrac{-15+8i}{4}.$$ It is not hard to realize that the RHS of the last equation is the square of $$\dfrac{1+4i}{2}.$$ Finally take the square root of both sides (do not forget both+ and -) and solve for the unknown $z.$

J. W. Tanner
  • 60,406
Bumblebee
  • 18,220
  • 5
  • 47
  • 87
1

Hint

You had the correct idea but you did the square root wrong.

$$\sqrt{(3-2i)^2-4(5-5i)}\ne 5$$

in fact,

$$\sqrt{(3-2i)^2-4(5-5i)}=\sqrt{-15+8i}=a+bi$$ with, $a,b \in \Bbb R$, so, $$(a+bi)^2=-15+8i$$

solve the above equation and get your result.

J. W. Tanner
  • 60,406
Arnaldo
  • 21,342
1

The OP made two errors in the exercise:

  1. As the quadratic formula is $\lambda= \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$, the $-(3-2i)$ should be replaced by $(3-2i)$ for $-b$.
  2. The calculation of $\Delta=b^2-4ac$ is incorrect.

We have

$$\Delta =b^2-4ac=(3-2i)^2-4(1)(5-5i)=(5-12i)-(20+20i)=-15+8i$$

so that

$$\lambda=\frac{3-2i\pm \sqrt{-15+8i}}{2}$$

where we can find the square roots $\pm (a+bi)$ of $-15+8i$ by solving the equation

$$(a+ib)^2=-15+8i$$

We have that $(1+4i)^2=-15+8i$, hence the two square roots are $\pm(1+4i).$ Therefore

$$\lambda=\frac{3-2i + (1+4i)}{2}=2+i$$

or

$$\lambda=\frac{3-2i - (1+4i)}{2}=1-3i$$

Axion004
  • 10,056